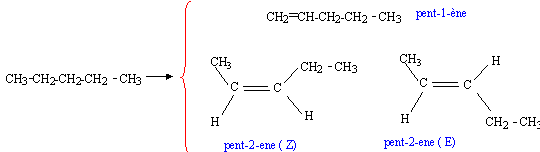
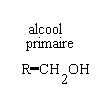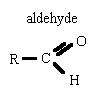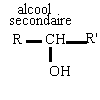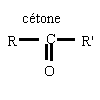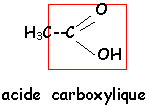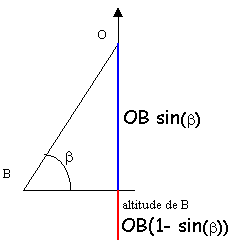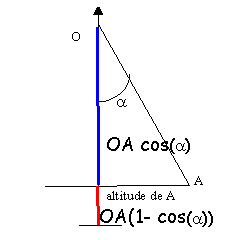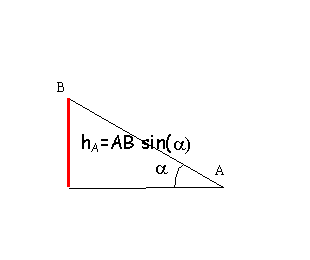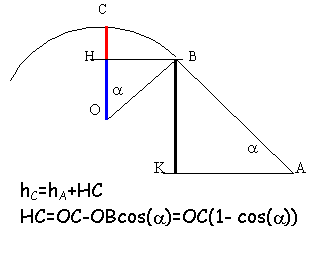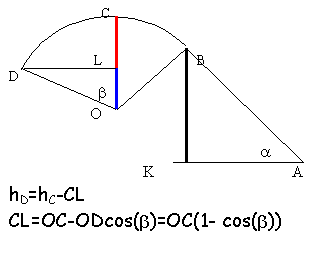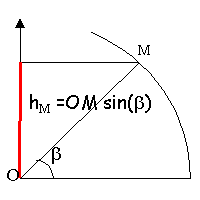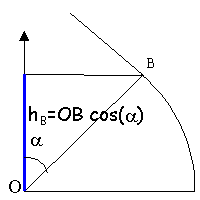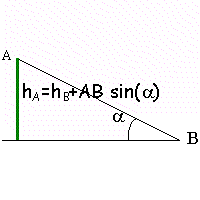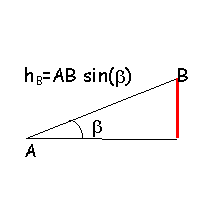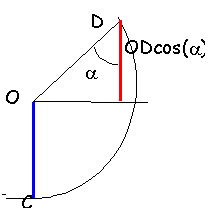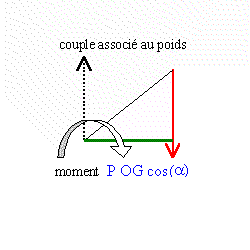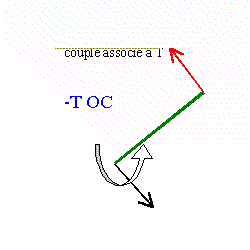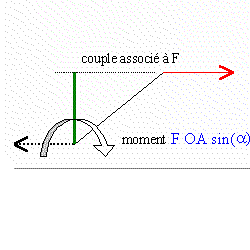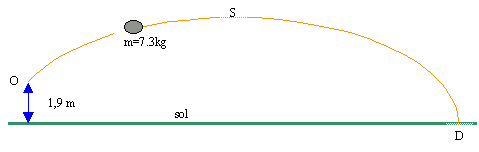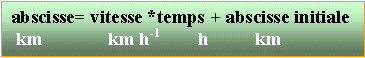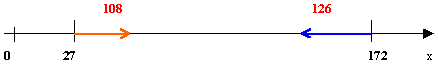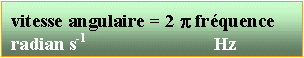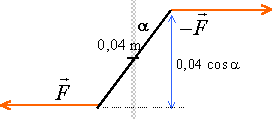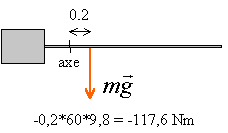- Ecrire les formules semi-développées des différents alcènes isomères de constitution, obtenus pas déshydrogéntation du pentane.
- L'un d'eux donne lieu à une isomérie d'un autre type. De quel type d'isomérie s'agit-il ? Représenter les isomères correspondants.
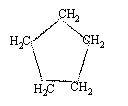
- Le reformage du pentane conduit à un hydrocarbure saturé, isomère des alcènes précédents. Quel est le produit ainsi formé? Justifier sa formation.
corrigé
reformage du pentane conduit à un hydrocarbure cyclique saturé le cyclopentane
|
|
Un insecticide est composé au niveau de la masse de 79,2% de chlore de 19,1% de carbone et de 1,6% d'hydrogéne.
- Trouver sa formule brute en sachant que sa masse molaire est comprise entre 200 et 400 g/mol.(Il est aussi marqué que pour 2 kg d'insecticide répandue il y a 1462 g de Cl)
C=12 ; H=1 ; Cl=35,5 g/mol
corrigé
fformule brute CxHyClz avec x, y, z entier
12 x / 19,1 =y /1,6 soit y= 12*1,6/19,1 x ; y = x
35,5 z/79,2 = y/1,6 soit z= 79,2/(1,6*35,5) y ; z =1,4 x
si x=5 alors z est entier
formule brute possible : C5H5Cl7.
masse molaire :12*5+5+35,5 *7 = 313,5 g/mol
|
|
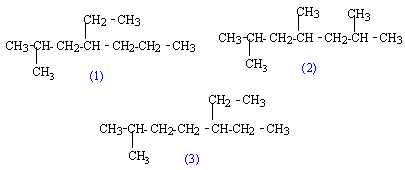
- Quel est le nom des l'hydrocarbures :
corrigé
(1) : 4-éthyl-2-méthylheptane
(2) : 2, 4, 6-triméthylheptane
(3) : 5-éthyl-2-méthylheptane
|
|
Trois alcools, quel'on notera A,B et C, ont été analysés : ils ont tous les trois la même formule brute: C4H10O . Pour déterminer leur formule semi-développée, on fait subir, sucessivement, à chacun des trois l'action d'une solution acidifiée de permanganate de potassium.on obtient les résultats suivants :
- l'alcool A, donne un unique corps que l'on notera D (que l'oxydant soit en défaut ou en excès)
- l'alcool B, donne deux corps, sucessivement: E avec dans un premier temps, puis F avec un excès d'oxydant
- l'alcool C, soumis à l'oxydant ne donne aucune réaction.
- Donner le bilan- simplifié- des réactions qui ont conduit à la formation de D d'une part, E et F d'autre part.
corrigé
2 fois{MnO4- + 5e- + 8 H+ --> Mn2+ + 4H2O}
l'alcool secondaire A s'oxyde en cétone D : 5 fois{ A--> D + 2e- + 2 H+}
2 MnO4- +16 H+ +5 A --> 2 Mn2+ + 8 H2O+ 5 D + 10 H+
2 MnO4- + 6 H+ +5 A --> 2 Mn2+ + 8 H2O+ 5 D
A est CH3-CHOH-CH2CH3 butan-2ol ; D la butanone CH3-CO-CH2CH3 CH3-CH2-CH2CH2OH
E est le butanal CH3-CH2-CH2CHO
F l'acide butanoïque CH3-CH2-CH2COOH
B s'oxyde en aldehyde E : 5 fois{ B--> E + 2e- + 2 H+}
2 MnO4- + 6 H+ +5 B --> 2 Mn2+ + 8 H2O+ 5 E
B s'oxyde en acide F : 5 fois{ B+ H2O--> F + 4e- + 4 H+}
4 fois{MnO4- + 5e- + 8 H+ --> Mn2+ + 4H2O}
4 MnO4- + 12 H+ +5 B -->4 Mn2+ + 11 H2O+ 5 F
C est un alcool tertiaire le 2,2-diméthylpropan-2-ol (CH3)3-C-OH
B est un alcool primaire par exemple le butan-1-ol |
|
On verse une petite quantité de méthanal dans quelques mL d'une solution d'ions diammine argent I (réactif de Tollens ) et on chauffe au bain-marie.la réaction a lieu dans un tube à essais.
- Décrire la réaction observée et donner le bilan simplifié de la réaction
- Le dépôt obtenu est pesé. Proposer une méthode opératoire simple pour effectuer cette pesée ;
- On trouve m= 1,8 g sachant qu'une mole d'aldehyde conduit à la formation de 2 moles de métal, calculer la masse de méthanal qui a réagi. on donne (en g.mol-1):C=12; O=16; H=1; Ag=108.
corrigé
la réaction observée est le test du miroir d'argent : l'argent se dépose sur les parois du tube à essai
l'ion diamine argent I se réduit en argent en présence d'un aldehyde
2[Ag(NH3)2]++2e- = 2Ag + 4NH3.
l'aldehyde R-CHO s'oxyde en acide carboxylique noté R-COOH
R-CHO+ H2O = RCOOH + 2H+ + 2e-
bilan : 2[Ag(NH3)2]++ R-CHO+ H2O = RCOOH + 2H+ + 2Ag + 4NH3.
il faut d'abord peser le tube à essai avant de commencer l'expérience et le peser à la fin
Qté de matière d'argent (mol) = masse (g) / masse molaire (g/mol) = 1,8 / 108 = 16,6 mmol
Qté de matière de méthanal (mol) = ½ Qté de matière (mol) d'argent = 8,3 mmol
masse molaire méthanal CH2O : 12+2+16 = 30 g/mol
masse de méthanal (g) = Qté de matière (mol) * masse molaire (g/mol) = 8,3 10-3*30 = 0,25 g.
|
|
L'hydratation de 2,1 g de propène conduit à un mélange de 2 alcools isomères A et B.
- Donner leurs formules et leurs classes.
- L'oxydation de l'alcool A par excès de permanganate de potassium, en milieu acide, conduit à une espèce chimique C que l'on peut extraire. C se dissout dans l'eau en donnant une solution de pH inferieur à 7.
- Identifier C.
- En déduire la formule de l'alcool A.
- Ecrire l'équation de l'oxydation de A en C.
- On dose la solution aqueuse de C avec une solution de soude de concentration 0,25 mol/l. L'équivalence est atteinte pour 24 mL de soude versée.
Calculer la quantité (en moles) de l'espèce C puis calculer celle de A.
- En déduire les proportions molaires des alcools A et B lors de l 'hydratation du propène .
corrigé
CH3-CHOH-CH3 propan-2-ol alcool secondaire
CH3-CH2-CH2 OH propan-1-ol alcool primaire (A)
l'alcool primaire (A) s'oxyde en acide acide propanoïque (C) CH3-CH2-COOH
(A) s'oxyde en acide (C) : 5 fois{ CH3-CH2-CH2 OH + H2O--> CH3-CH2-COOH + 4e- + 4 H+}
4 fois{MnO4- + 5e- + 8 H+ --> Mn2+ + 4H2O}
4 MnO4- + 12 H+ +5 CH3-CH2-CH2 OH -->4 Mn2+ + 11 H2O+ 5 CH3-CH2-COOH
0,25*24 10-3 = 6 10-3 mol
donc 0,006 mol de A
Qté de matière de propène C3H6 ( M=3*12+6=42 g/mol) : 2,1 / 42 = 0,05 mol
donc 0,05-0,006 = 0,044 mol B.
à l'équivalence la quantité de matière d'acide est égale à la quantité de matière de soude
|
|
300 mg d’un composé organique noté A de formule CxHyOz est oxydé totalement en donnant 887 mg de CO2 et 340 mg d’eau.
- Calculer les pourcentages massiques de C, H et O.
- Sachant que la masse molaire est M= 238 g.mol -1, déterminer la formule brute de ce composé organique.
corrigé
masse molaire de CO2=44g/mol
dedans le C compte pour 12g
la proportion est 12/44 de C dans la masse de CO2 donc masse de carbone dans A mC=12/44*0,887 =0,242 g.
% de C dans l'échantillon :0,242/300*100 = 80,64 %
de même : la masse molaire de H2O est 18 g/mol ; mH= 2/18*mH2O=0,34/9 = 0,038 g
% de H dans l'échantillon :0,038/300*100 = 12,59 %
% de O dans l'échantillon : 100-80,64-12,59 = 6,77 %.
la masse molaire de ce composé A est: 12x+ y+ 16z=238g/mol
donc %C=12x/238*100 soit x= %C*2,38/12 = 16
%H= y/238*100 soit y= %H*2,38 = 30.
%O= 16z/238*100 soit z = %O*2,38/16 =1.
| alcool : le groupe OH est fixé sur un carbone tétragonal
primaire R-CH2OH secondaire R-CHOH -R' tertiaire RR'COHR"
|
| aldehyde réducteur
la liqueur de Fehling bleue donne un solide rouge brique Cu2O
l'ion diammineargent est réduit en argent
le réactif de Schiff devient rose
|
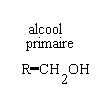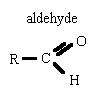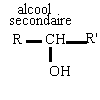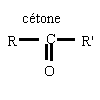
l'oxydation ménagée des alcools conserve le squelette carboné
|
| le groupe carbonyle >C=O des aldehydes et des cétones
donne avec la DNPH un solide jaune
|
|
|
|
|
| exercice 1 |
stéréochimie: hydratatation d'alcènes |
| L'addition d'eau a un alcène conduit à un ou plusieurs alcools noté P ; ce dernier contient en masse 21 % d'élément oxygène
CnH2n + H2O donne CnH2n+2O
- Quelle est la formule brute de P ?
- L'alcool P contient un carbone asymétrique . Identifier P.
- Quels alcènes conduisent à P par addition d'eau ?
corrigé
|
| 16/0,21 = M
avec M=14n
|
Les deux derniers rapports de la formule ci contre conduisent à n=4 alcène C4H10
|
|
|
Un carbone asymétrique doit être relié à 4 groupes d'atomes différents
|
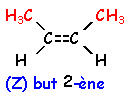 |
Aux alcénes ci contre , il faut ajouter le but-1-ène H2C=CH-CH2-CH3. |
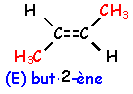 |
|
|
|
| exercice 2 |
oxydation ménagée de composés organiques |
|
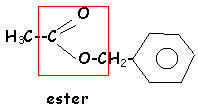
L'hydrolyse de A (C9H10O2 ) conduit à un acide carboxylique C et à un alcool D.
- Quelle fonction chimique possède A ?
- La formule de C est C2H4O2 Donner son nom et écrire sa formule semi développée.
- Quelles sont les caractéristiques de la réaction ci dessus ?
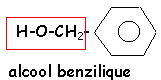
- Quelle est la formule brute de D , Il s'agit d'alcool benzilique, écrire sa formule semi développée.
- Ecrire la formule semi développée de A.
corrigé
|
| A posséde une fonction ester. L'hydrolyse de cet ester est lente , athermique , limitée.
|
|
|
| exercice 3 |
Oxydation ménagée et combustion |
- Oxydation ménagée de l'éthanol(oxydant en défaut). Ecrire l'équation bilan de la réaction. Quel est le nom du produit ? Comment peut-on mettre en évidence sa présence
- Combustion complète de l'éthanol. Ecrire l'équation bilan de cette réaction.
- On effectue la combustion incomplète dans les CNTP de 4 moles de propanone dans un volume de dioxygène de 67,2L.
- Ecrire l'équation bilan de la réaction.
- En déduire le nombre de moles des réactifs restant et des produits formés.
- Trouver la masse de carbone formé lors de cette combustion. C=12 gmol-1.
corrigé
|
| oxydation ménagée :
conservation du squelette carboné
CH3-CH2-OH + 1/2O2 ---> H2O + CH3-CHO ethanal combustion complète
CH3-CH2-OH + 3O2 ---> 3H2O + 2 CO2
combustion incomplète
CH3-CO-CH3 + O2 ---> 3H2O + 3 C
3 moles de O2 réagissent avec 3 moles propanone en donnant 9 moles d'eau et 9 moles de carbone (9*12=108g). Il reste 1 mole de propanone.
|
|
CHIMIE :concours kiné 99 Grenoble quelques exercices
physique :concours kiné 99 Grenoble
|
| exercice 1 |
solution d'hydroxyde de sodium
|
|
|
|
On dissout 2 mg d'hydroxyde de sodium solide dans 500 mL d'eau à 25°C
masse atomique molaire gmol-1 Na=23 O=16 H=1
Le pH de la solution obtenue est de 2 ; 12 ; 8 ; 14 ; 10
|
|
|
|
|
|
| Qté de matière d'ion hydroxyde (mol) |
2 10-3 /40 |
5*10-5 |
| concentration [OH-] molL-1 |
5*10-5 /0,5 |
10-4 |
| [H3O+]*{OH-]=10-14 |
[H3O+] |
10-10 |
| pH=-log([H3O+]) |
10 |
|
|
|
| exercice 2 |
dosage acide fort base forte
|
|
|
On dose 20 ml d'une solution d'acide chlorhydrique par la soude à0,01 molL-1 en présence de BBT. Le virage de l'indicateur se produit pour un volume de base de 9 mL .
La concentration initiale de l'acide est: 90 mmolL-1 ; 4,5 mmolL-1 ; 4,5 molL-1
|
|
|
|
|
|
| Qté de matière d'ion hydroxyde (mol) |
0,01*910-3 |
910-5 |
| à l'équivalence qté de matière d'ion hydronium (mol) |
910-5 |
|
| concentration de l'acide molL-1 |
910-5/20 10-3 |
4,5 10-3 |
|
| exercice 3 |
dosage acide faible base forte demi équivalence
|
|
|
A 100 mL dacide éthanoique à 0,1 molL-1, on ajoute 100 mL de soude à 0,005 molL-1. On obtient 200 mL de solution dont le pH est: 7; 4,75 ; 1,17 ; 1,2 ; 12
pKa(ac éthanoique/ ion éthanoate)=4,75
|
|
|
|
|
|
| Qté de matière d'ion hydroxyde (mol) |
0.1*0,05 |
5 10-3 |
| Qté de matière d'acide éthanoique (mol) |
0,1*0,1 |
0,01 |
| arrèt à la demi équivalence du dosage acide faible base forte |
pH=pKa=4,75 |
|
|
|
| exercice 4 |
constante d'une réaction acide base
|
|
|
Un litre de solution d'engrais pour plante est préparé en dissolvant 0,1 mol de phosphate d'ammonium solide (NH4)3PO4 dans la quantité d'eau nécessaire. La consatnte de réaction entre les ion ammonium et phosphate est:1580 ; 3,2 ; 1,72 ; 1,58 10-3
pKa(NH4+/NH3 )=9,2 ; pKa(HPO42-/PO43-)=12,4
|
|
|
|
|
|
| l'ion ammonium, acide le plus fort réagit avec l'ion phosphate, la base la plus forte |
| donc la constante de cette réaction naturelle est assez grande |
|
|
|
10-9,2 / 10-12,4 |
103,2=1585 |
|
|
|
|
| exercice 5 |
trouver la formule brute d'un ester
|
|
|
L'analyse d'un ester conduit aux pourcentages massiques suivants: 58,8% de carbone 31,4% d'oxygène et 9,8% d'hydrogène .Masse atomique molaire en g mol-1 C=12 ; O=16 ; H=1
La masse molaire de l'ester est: 90 ; 51 ; 102 ; 120 ; 142
|
|
|
|
|
|
| formule brute d'un ester CnH2nO2 |
 |
|
|
n=5 |
102 |
|
|
|
|
|
|
| exercice 6 |
chlorure d'acyle + alcool ---> ester + HCl
|
|
|
Le chlorure d'éthanoyle réagit sur le 3-méthylbutane-1-ol en donnant un corps X et du chlorure d'hydrogène. La masse du chlorure d'éthanoyle ayant réagi est de 31,4 g. La masse du produit X formé est (g) :88,5 ; 78,5 ; 131 ; 52 ; 108
Masse atomique molaire en g mol-1 C=12 ; O=16 ; H=1 ;Cl=35,5
|
|
|
|
|
|
 |
| Qté de matière chlorure d'acyle (mol) |
31,4 / 78,5 |
0,4 |
| X est l'éthanoate de 3-méthylbutane C7H14O2 |
0,4*130 |
52g |
|
|
| exercice 7 |
masse volumique d'un gaz
|
|
|
On remplit une bouteille plastique de 1,5 L de dihydrogène. Dans les conditions de l'expérience le volume molaire d'un gaz est 24 Lmol-1. La masse volumique en gL-1 du dihydrogène est dans ces conditions égale à: 4,12 10-2 ; 8,33 10-3 ; 1,33 ; 0,67 ; 1,75
|
|
|
|
|
|
| Qté de matière de dihydrogène en mol |
1,5 / 24 |
0,0625 |
| masse de dihydrogène en g |
0,0625*2 |
0,125 |
| masse volumique g/L |
0,125 /1,5 |
0,0833 |
|
|
| exercice 8 |
combustion du butane réactif en excès
|
|
|
On mélange 5,8 g de butane et 10 L de dioxygène . La combustion complète de ce mélange donne du dioxyde de carbone et de l'eau. La masse d'eau liquide produite est (g) 4,5 ; 9 ; 5,4 ; 5,8 ; 11
volume molaire 25Lmol-1 Masse atomique molaire en g mol-1 C=12 ; O=16 ; H=1
|
|
|
|
|
|
| C4H10 +6,5 O2 donne 4 CO2 +5 H2O |
|
| Qté de matière de butane en mol |
5,8 /58 |
0,1 |
| Qté de matière dioxygène en mol |
10 / 25 |
0,4 |
| à partir de 0,1 mol de butane il faut 0,65 mol dioxygène |
excès butane |
|
| à partir de 0,4 mol dioxygène il se forme 0,4*5 /6,5 mol d'eau |
0,307*18 |
5,4 g |
|
|
| exercice 9 |
pourcentage massique et densité
|
|
|
On dispose d'une bouteille de 0,5 L d'une solution commerciale d'acide nitrique . L'étiquette de la bouteille porte les indications suivantes : densité 1,33 pourcentage massique en acide 52,5%. La concentration molaire de la solution commerciale est: 2,2 10-2 ; 8,33 ; 5,54 ; 11,08 ; 16
acide nitrique HNO3 Masse atomique molaire en g mol-1 N=14 ; O=16 ; H=1
|
|
|
|
|
|
| masse d'acide dans 1 litre |
0,525*1330 |
698 g |
| Qté de matière d'acide dans un litre |
698 / 63 |
11,08 mol |
| concentratin de l'acide molL-1 |
11,08 |
|
| 1 litre de solution de densité 1,33 a une masse de 1330 grammes |
|
|
| exercice 10 |
acide chlorhydrique et alliage nickel cuivre
|
|
|
Un alliage nickel cuivre est attaqué à froid par de l'acide chlorhydrique en excès . la masse de l'alliage est 3 g . On recueille 427,4 ml de dihydrogène dans les conditions normales de tempèrature et de pression . On donne les potentiels redox Ni2+/Ni -0,23 V ; Cu2+/Cu 0,34V ; H+/H2... 0V. La masse en gramme de résidu solide après réaction est : 0 ; 4,7 ; 4,88 ; 1,79 ; 1,88
Masse atomique molaire en g mol-1 Ni=58,7 ; O=63,5
|
|
|
|
|
|
| Ni + 2H3O+ donne H2 + Ni2+ + 2 H2O |
cuivre non attaqué |
| Qté de matière de dihydrogène en mol |
0,4274 / 22,4 |
0,0191 |
| Qté de matière de nickel attaqué en mol |
|
0,0191 |
| masse de nickel attaqué en g |
0,0191*58,7 |
1,12 g |
| le résidu est le cuivre |
3-1,12 |
1,88 g |
|
|
| exercice 11 |
variation de masse des électrodes d'une pile
|
|
|
Les demi-équations électroniques qui se produisent aux électrodes d'une pile sont: Cr donne Cr3+ +3e- Pb2+ + 2e- donne Pb. La perte de masse de l'électrode en chrome est 1,56 g . La masse de plomb déposée à l'autre électrode est: (g): 9,32 ; 6,24 ; 1,56 ; 18,71 ; 3,12
Masse atomique molaire en g mol-1 Cr=52 ; Pb=207,2
|
|
|
|
|
|
| 3 Pb2+ +2 Cr donne 3 Pb + 2 Cr3+ |
|
|
| Qté de matière de chrome perdue en mol |
1,56/52 |
0,03 |
| Qté de matière de plomb gagnée en mol |
0,03 /2 *3 |
0,045 |
| masse de plomb déposée en grapmme |
0,045*207,2 |
9,32 |
|
|
|
|
|
|
|
|
| exercice 12 |
argenter une plaque métallique par électrolyse
|
|
|
L'une des 2 électrodes est constituée par l'objet métallique . L'électrolyte est une solution de sulfate d'argent(I) . La surface à argenter est 0,25 m2, l'épaisseur de la couche à déposer est égale à 0,015 mm . La masse volumique de l'argent est 10500kgm3 . L'intensité du courant qui traverse l'électrolyseur est 60A . masse atomique molaire gmol-1 Ag=108 un faraday = 96500 coulombs . La durée de l'électrolyse pour éffectuer ce dépot est: 9 min47s ; 84,6 h ; 304,6 min ; 84,6 min ; 15 min
|
|
|
|
|
|
| volume d'argent (m3) |
0,25*1,5 10-5 |
3,75 10-6 |
| masse d'argent ( kg) |
3,75 10-6*10500 |
0,03937 |
| Qté de matière d'argent en mol |
0,03937*1000/108 |
0,3645 |
| Qté de matière d'électrons (mol) |
0,3645 |
|
| la charge d'une mole d'électrons est 96500 coulombs |
0,3645*96500
|
35182 C |
| durée (s) * intensité (A)=35182 |
durée 586,3s |
9 min 47s |
|
|
| exercice 13 |
pluies acides
|
|
|
Une installation de chauffage utilise 3600 L de fuel (densité 0,9) par an contenant en masse 0,3% de soufre . Elle rejette du dioxyde de soufre dans l'atmosphère . Ce dernier se transforme en acide sulfurique 2S +3O2 +2H2O donne 2 H2SO4 . La masse (kg) d'acide sulfurique formée annuellement est 992,7 ; 29,8 ; 59,6 ; 14,9 ; 2980 masse atomique molaire gmol-1 S=32 ; O=16 ; H=1
|
|
|
|
|
|
| masse de fuel (kg) |
3600*0,9 |
3240 |
| masse de soufre (kg) |
3240*0,3/100 |
9,72 |
| Qté de matiére de soufre (mol) |
9720 / 32 |
303,7 |
| Qté de matière acide sulfurique (mol) |
303,7 |
|
| mased'acide sulfurique (kg) |
303,7*(2+32+48)
|
29,76 |
|
|
| exercice 14 |
oxydation par le permanganate de potassium
|
|
|
On dose en milieu acide 20 mL d'une solution de fer(II) par une solution de permanganate de potassium à 1,8 10-2 molL-1 . Il faut verser 14,6 mL de cette solution pour observer une coloration rose persistante. MnO4- + 8H+ + 5 e- donne Mn2+ + 4H2O et Fe2+ donne Fe3+ + 1e- . La concentration en ion fer (II) est en molL-1 : 0,12 ; 0,013 ; 0,025 ; 0,018 ; 6,6 10-2
|
|
|
|
|
|
| MnO4- + 8H+ + 5 Fe2+ donne 5 Fe3++ Mn2+ + 4H2O |
|
| Qté de matière d'ion permanganate (mol) |
0,0146*0,018
|
2,628 10-4 |
| Qté de matière d'ion fer(II) mol |
5*2,628 10-4 |
1,314 10-3 |
| concentration d'ion fer (II) molL-1 |
1,314 10-3 / 0,02
|
0,0657 |
effets de la chaleur- augmentation de la température sans changement d'état physique
Q = m c Dq
Q: joule ; m kg ; Dq degré
c: capacité thermique massique J kg-1 K-1
mc: capacité thermique J K-1
pour élever de 1° la température de 1 kg de cuivre il faut fournir 385 J
pour élever de 1° la température de 1 kg d'eau il faut fournir 4180 J
changement d'état physique à température constante
Q = mL
L : chaleur latente de changement d'état physique à température constante J kg-1
à 0°, la fusion de 1 kg d'eau nécessite 335 kJ
à 100° la condensation de 1 kg de vapeur d'eau libère 2 262 kJ
|
|
|
|
| exercice 1 |
four électrique |
Cent tonnes de ferrailles sont chauffées dans un four électrique afin d'obtenir du fer liquide à 1535°C. La température initiale est 20°C. La durée de l'opération dure 5 heures et le rendement du four est de 70%. Cfer=450 Jkg-1 K-1. Lfusion fer= 270 kJ kg-1.
- Quelle est l'énergie nécessaire. En déduire la puissance du four.
|
| corrigé |
|
Energie (J) nécessaire à :
- porter le solide de 20 à 1535°C: mcDq = 105*450*1515= 6,8 1010 J
- fusion du fer à 1535°C : mL = 105*2,7 105= 2,7 1010 J
total : 9,5 1010 J
en tenant compte du rendement
9,5 1010 / 0,7 = 1,36 1011 J
puissance (watt)=énergie(J) / durée(seconde)
P = 1 36 1011 / (5*3600) = 7,5 106 W
|
|
|
|
| exercice 2 |
fusion de la glace |
|
|
100g de glace prise à -10°C sont chauffés dans un récipient. Le dispositif de chauffage à un rendement de 80% et sa puissance est P=2kW. On coupe le chauffage lorsque toute la glace est fondue, l'eau de fusion étant à 0°C. Quelle est la durée du chauffage ?
C glace=2100 JK-1 ; Lfusion glace =330 kJkg-1.
|
| corrigé |
|
Energie (J) nécessaire à :
- porter le solide de -10 à 0°C: mcDq = 0,1*2100*10= 2,1 103 J
- fusion de la glace à 0°C : mL = 0,1*3,3 105= 3,3 104 J
total : 3,51 104 J
en tenant compte du rendement
3,51 104 / 0,8 = 4,39 104 J
puissance (watt)=énergie(J) / durée(seconde)
temps= 4, 39 104 / 2000 = 22 s
|
|
|
| exercice 3 |
chaleur de réacion NaOH + HCl |
| Dans un calorimètre (200JK-1), on mélange 0,1 L de solution de soude à 2 molL-1 et 0,1L de solution d'ac. chlorhydrique à 2 molL-1. L'augmentation de température est de 43 °C lors de la réaction.
C solution=4180 Jkg-1K-1. NaOH=40 ; HCl=36,5 gmol-1.
- Calculer la masse des réactifs, l'énergie libérée lors de la réaction, l'énergie libérée par mole de réactif.
|
corrigé |
masse
Qté de matière mole = volume(L) * concentration (mol L-1)
0,1*2=0,2 mol soit 40*0,2=8 g de soude et 0,2*36,5 = 7,3 g acide
total 15,3 g=0,0153 kg chaleur libérée
mcDq= (0,0153*4180 + 200)*43 = 11350 J pour 0,2 mol de chaque réactif
ou bien 11350*5= 57 kJ mol-1. réaction exothermique
|
| |
|
|
|
| exercice 4 |
déterminer une capacité thermique massique |
|
Dans un calorimètre (200JK-1), contenant 200g d'eau à 18°C, on plonge 100g de cuivre pris dans une étuve à 80°C. C eau=4180 Jkg-1K-1. La tempèrature d'équilibre est 20,2 °C. Quelle est la capacité thermique massique du cuivre ?
|
|
| corrigé |
|
Energie
- gagnée par le calorimètre et l'eau qu'il contient: (200 + 0,2*4180)2,2= 2235 J
- cédée par le cuivre 0,1*C*(80-20,2)=5,98 C
L'énergie cédée par le cuivre est gagnée par l'eau et le calorimètre.
2235=5,98 C ........Ccuivre = 376 Jkg-1K-1.
|
|
|
|
|
| exercice 5 |
|
- Un calorimètre contient une masse m1= 500g d'eau à température t1=19°C. On y introduit une masse m2= 150g d'eau à la température t2=25,7°C. La température finale est tf=20,5°C. Calculer la capacité thermique du calorimètre ?C eau =4180 JK-1 kg-1
- Dans le même calorimètre contenant maintenant 750g d'eau à 19°C, on immerge un bloc de cuivre de 550g porté à 92°C . La température finale est 23,5°C. Quelle est la capacité thermique massique du cuivre?
- Quelle quantité de soda peut on refroidir de 30°C à 10 °C avec un cube de glace de 25g qui sort du réfrigérateur à 0°C? C soda =4180 JK-1 kg-1. chaleur latente de fusion de la glace:Lf=335 kJkg-1.
corrigé
|
| L'eau chaude transfert la chaleur Q1 au calorimètre et à l'eau qu'il contient :
Q1 = 0,15*4180*(25,7-20,5)= 3260,4 J
capacité thermique de :
l'eau froide : 0,5*4180=2090 JK-1.
du calorimètre : m
total : m + 2090
chaleur gagnée par les corps froids :
Q2=(m + 2090)*(20,5-19)=1,5 m + 3135
1,5 m + 3135 =3260,4
m = 83,3 JK-1. Le cuivre transfert la chaleur Q1 au calorimètre et à l'eau qu'il contient :
Q1 = (0,75*4180 + 83,3)*(23,5-19)= 14482 J
chaleur cédée par le cuivre:
Q2=0,55 * c *(92-23,5)= 37,67 c
37,67 c =14482
c = 384,4 JK-1kg-1. Le soda transfert de la chaleur à la glace qui fond à 0°C puis l'eau de fusion se réchauffe .
chaleur cédée par le soda : m*4180*(30-10)= 83600 m
chaleur nécessaire à :
la fonte de la glace :0,025*335 000= 8375 J
25 g d'eau se réchauffe : 0,025*4180*(10-0)=1045 J
total : 9420 J
c = 9420 / 83600 = 112,7 g
|
|
|
|
| exercice 6 |
|
- L'eau d'une rivière à température 16°C est utilisée pour la condensation de la vapeur d'eau usée d'une centrale nucléaire. La température initiale de la vapeur est 130°C. La température de l'eau à la sortie de la condensation vaut 60°C. Quelle est la quantité d'eau de la rivière nécessaire pour condenser 1Kg de vapeur? Chaleur de vaporisation de l'eau:2 260 kJkg-1.C vapeur d'eau: =2090JK-1kg-1. Ceau liquide=4180JK-1kg-1.
- Une maison bien isolée de surface 90m2 a une hauteur sous plafond de 2,5m. Le chauffage est réglé pour que la température intérieure soit égale à 21°C. La température extérieure vaut 10°C. Calculer la puissance perdue si toutes les 3 heures, tout l'air de la maison est renouvelé par l'air extérieur. Cair =1kJK-1kg-1.Masse volumique de l'air à 20°C:1,2 kgm-3.
corrigé
|
| La vapeur d'eau transfert de la chaleur à l'eau de la rivière.
chaleur cédée par 1 kg de vapeur :
la vapeur se refroidit : 2090*(130-100)= 62700 J
la vapeur se condense à 100 °C : 2 260 000 J
1kg d'eau se refroidit : 4180*(100-60)= 167 200 J
total : 2,49 106 J
m kg d'eau de la rivière gagnent :
m*4180*(60-16)= 183 920 m
m= 2,49 106 /183 920 = 13,54 kg masse (kg) d'air contenu dans la maison : volume(m3)* masse volumique de l'air kgm-3.
90*2,5 *1,2 = 270 kg
Chaleur gagnée par l'air extérieur :
270* 1000*(21-10)= 2,97 106 J
puissance perdue (watt)=énergie(J)/ durée (seconde)
2,97 106 /(3*3600)= 275 W
|
|
On se propose de déterminer expérimentalement la variation d’énergie interne de 1g d’eau liquide lorsque sa température augmente de 1°C.
Pour cela, on apporte de l’énergie par mode travail mécanique à de l’eau contenue dans un calorimètre (un calorimètre est un vase très bien calorifugé, c’est à dire qu’il limite au mieux le transfert thermique entre l’intérieur du vase et le milieu environnant)
Deux cylindres D et D’ ont chacun une masse M. Pendant leur descente qui s’effectue sur la hauteur h , elles entraînent en rotation un ensemble de palettes dans l’eau du calorimètre ; on remonte ces cylindres avec une manivelle, et pendant la remontée, un système de découplage permet de ne plus entraîner les palettes qui alors sont immobiles. Pendant la descente, le système mécanique qui transforme le mouvement de translation des masses en mouvement de rotation des palettes a un rendement énergétique de 45%.
- Etablir la variation d’énergie d’un cylindre D ou D’ pendant la remontée sur la hauteur h ; quelle est la nature de cette énergie ?
- Etablir l’expression de la variation d’énergie interne de l’eau du calorimètre au bout de n descentes.
- Pour l’application numérique M = 1,00 kg ; h =1,5 m ; le volume d’eau dans le calorimètre est 0,50 L ; on constate qu’après n = 140 descentes , la température de l’eau s’est élevée de 0,89 °C.
- Calculer la valeur de la variation d’énergie interne de l’eau du calorimètre.
- Quelle est la valeur de la variation d’énergie interne de 1 g d’eau liquide lorsque sa température augmente de 1°C ?
corrigé
variation d’énergie d’un cylindre D ou D’ pendant la remontée sur la hauteur h :
c'est la variation d'énergie potentielle D Ep=Mgh ; nature, c'est de l'energie était mécanique.
L'énergie interne est l'énergie emmagasinée par un système, autre que l'énergie cinétique macroscopique et l'énergie potentielle due à l'action des corps extérieurs.
Energie transmise à l'au à chaque descente d'un cylindre : rendement * variation d'énergie potentielle de pesanteur
et pour n descentes : n*rendement* variation d'énergie potentielle de pesanteur = n *0,45 Mgh
Energie transmise au 0,5 litre l'eau par 1 descente d'un cylindre = 0,45 * 1 * 9,81 * 1,5 = 6,622 J
Il y a 140 descentes et 2 cylindres -> 140 * 2 * 6,62175 = 1854 J.
cette énergie est calculée pour 500 g d'eau, soit :
1854 / 500 = 3,71 J pour 1 g d'eau ( ou pour 1 cm3 d'eau)
Cette énergie élève la température de 0,89°C
Pour élever le température de 1 cm³ d'eau de 1°C, il faut donc 3,71/0,89 = 4,17 J.
|
|
- Ecrire la réaction de formation de l'eau liquide à 298 K en précisant l'état physique des réactifs.
- Lorsqu'elle se déroule à 298 K la réaction de combustion du dyhidrogene est elle différente de la réaction précédente?
- L'enthalpie molaire standard de cette reaction vaut -285,2 kJ.mol-1. Cette réaction est elle endothermique ou exothermique?
- Quelle quantité de dyhidrogène faut il bruler sous la pression standard pour élever de 2 852 J l'énergie interne d'un bloc de cuivre ? On supposera qu'il n'y a pas de deperdition de chaleur.
- Quel volume de ce gaz supposé parfait mesuré sous P=1 bar et à 298 K faut il utiliser?
Données R= 8.314 J.mol-1.K-1 ;1 bar = 10 5Pa
corrigé
à 298 K : H2(g) +1/2 O2(g) ---->H2O(l)
à 298 K la réaction de combustion du dyhidrogene est la réaction précédente.
le signe - correspond à de l'énergie cédée par le système, la réaction est exothermique.
2852 J = 2,852 kJ ce qui correspond à 0,01mole de dihydrogène.
PV=nRT ; V=nRT/P = 0,01 *8,31*298 / 105 =2,47 10-4 m3.
|
|
| |
| exercice 1 |
oscillations d'un pendule |
| frottements négligeables. Un bille de masse m est suspendue à un fil de masse négligeable. L'origine de l'énergie potentielle de pesanteur est le point le plus bas.
m=200 g; OA=0,5 m ; a=0,6rad ; b=1 rad.
vitesse initiale en A : 7,2 km h-1.
1 m s-1 =3,6 km h-1.
- Calculer les altitudes de A et B
- Calculer l'énergie mécanique en A
- Calculer la vitesse en B en km h-1.
- la masse de la bille double, que deviennent
- l'énergie mécanique ?
- la vitesse en B ?
|
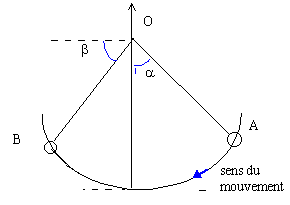 |
corrigé |
| altitude de A
OA(1-cos(a)= 0,0873 m
altitude de B
OB(1-sin(b)= 0,0793 m
énergie mécanique en A
somme de l'énergie cinétique et de l'énergie potentielle de pesanteur
0,5 mvA² + mg OA(1-cos(a)
danger!!!! vitesse en m s-1
0,571 J
|
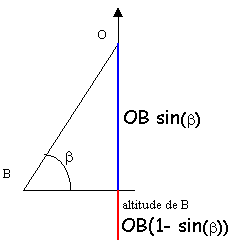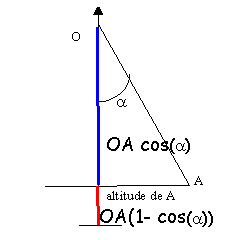 |
| vitesse en B
énergie mécanique en B: 0,571 J
énergie potentielle en B: 0,2*9,8*0,0793 = 0,155 J
énergie cinétique en B: 0,416 J
vitesse en B: rac carrée (0,416 *2 / 0,2)
2,04 m s-1 = 2,04*3,6=7,34 km h-1.
L'énergie mécanique étant proportionnelle à la masse, si la masse double, alors l'énergie mécanique double.
Que devient la vitesse en B si la masse double ?
énergie mécanique en A = énergie mécanique en B
0,5mvA²+ mg altitude A = 0,5mvB²+ mg altitude B
0,5vA²+ g altitude A = 0,5vB²+ g altitude B
La vitesse en B est indépendante de la masse , vB ne change pas
|
|
|
| exercice 2 |
plan incliné au sommet arrondi |
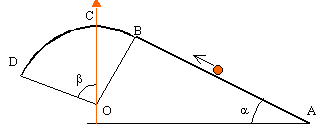
| frottements négligeables. Un bille de masse m lancée de A à la vitesse V se déplace vers D. L'origine de l'énergie potentielle de pesanteur est le point le plus bas A.
m=1 kg; OB=0,5 m ;AB=2 m ; a=0,3rad ; b=0,9 rad.
vitesse initiale en A : 18 km h-1.
1 m s-1 =3,6 km h-1.
- Calculer les altitudes de B , C et D.
- Calculer l'énergie mécanique en A
- Calculer la vitesse en D en km h-1.
- la vitesse initiale est divisée par deux, que deviennent
- l'énergie mécanique ?
- la vitesse en C et en D ?
|
 |
corrigé |
| altitude de B
hB =AB sin(a)= 0,591 m
altitude de C
hC =hB+ OB(1-cos(a)= 0,6133 m
altitude de D
hD =hC -OB(1-cos(b)= 0,424 m
énergie mécanique en A
entierement sous forme d'énergie cinétique
0,5 mvA²
danger!!!! vitesse en m s-1
12,5 J
|
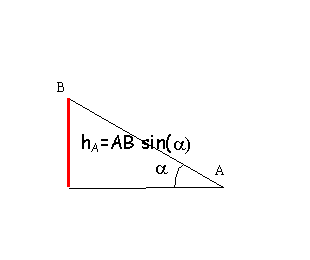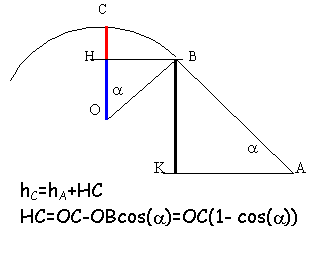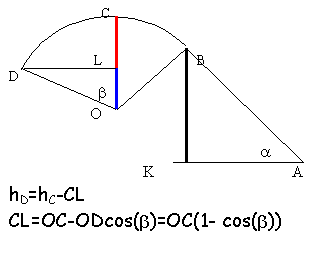
|
| vitesse en D le point D est atteint si on passe en C(sommet)
énergie mécanique en C: 12,5 J
énergie potentielle en C: 1*9,8*0,6132 = 6 J
énergie cinétique en C: 6,5 J on passe au sommet après ça descend
énergie potentielle en D: 1*9,8*0,424 = 4,155 J
énergie cinétique en D: 8,345 J
vitesse en D: rac carrée (8,345 *2 / 1)
4,08 m s-1 = 4,08*3,6=14,7 km h-1.
l'énergie mécanique est sous forme cinétique, proportionnelle au carré de la vitesse; si la vitesse est divisée par 2, alors l'énergie mécanique est divisée par 4.
Que devient la vitesse en D dans ces conditions ?
Le point C (sommet) est il atteint ?
énergie mécanique en A = énergie mécanique en C
0,5mvA²= 0,5mvC²+ mg altitude C
12,5 / 4 = 0,5mvC²+9,8*0,6132
0,5mvC² =3,125 -6 = -2,87 impossible un carré doit être positif !!!!
le sommet C n'est pas atteint, pas plus que D.
En A |
|
| exercice 3 |
descente d'une piste |
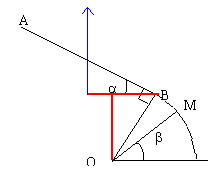
| frottements négligeables. Un bille de masse m lancée de A à la vitesse V se déplace vers M. L'origine de l'énergie potentielle de pesanteur est le point le plus bas O. Le solide décolle après être passé en M.
m=1 kg; OB=0,8 m ;AB=2 m ; a=0,1 rad ; b=1,06 rad.
vitesse initiale en A : 3,6 km h-1.
1 m s-1 =3,6 km h-1.
- Calculer les altitudes de A , B et M.
- Calculer l'énergie mécanique en A
- Calculer la vitesse en M en km h-1.
- la vitesse initiale est nulle, que deviennent
- l'énergie mécanique ?
- la vitesse en B ?
|
 |
corrigé |
| altitude de B
hB =OB cos(a)= 0,796 m
altitude de M
hM = OM sin(b)= 0,698 m
altitude de A
hA =hB + AB sin(a)= 0,9956 m
énergie mécanique en A
somme de l'énergie potentielle et de l'énergie cinétique
mghA+0,5 mvA²
danger!!!! vitesse en m s-1
10,26 J
|
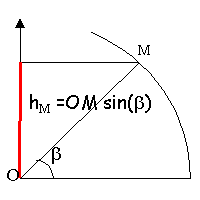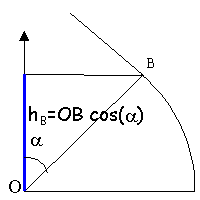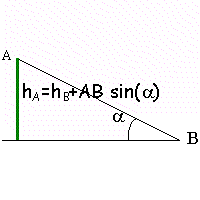
|
vitesse en M
énergie mécanique en M: 10,26 J
énergie potentielle en M: 1*9,8*0,698 = 6,84 J
énergie cinétique en M: 3,42 J
vitesse en M: rac carrée (3,42 *2 / 1)
2,615 m s-1 = 2,615*3,6=9,415 km h-1.
l'énergie mécanique est sous forme potentielle
9,75 J
vitesse en B
énergie mécanique en A = énergie mécanique en B
9,75= 0,5mvB²+ mg altitude B
9,75 = 0,5mvB²+9,8*0,796
0,5mvB² =1,95
1,97 m s-1
En A |
|
| exercice 4 |
bille sur une glissière |
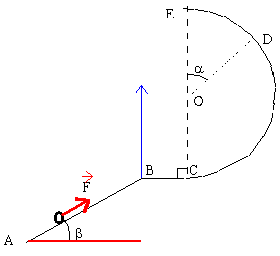
| frottements négligeables. Un bille de masse m lancée de A à la vitesse V se déplace vers D. L'origine de l'énergie potentielle de pesanteur est le point A. Une force constante de valeur F=2 N agit entre A et B; l'énergie mécanique en A augmente de F*AB sur le trajet AB.
m=100 g; OD=1 m ;AB=2 m ; a=0,5 rad ; b=0,2 rad.
vitesse initiale en A : 7,2 km h-1.
1 m s-1 =3,6 km h-1.
- Calculer les altitudes de B et D.
- Calculer l'énergie mécanique en A et en B
- Calculer la vitesse en C puis en D en km h-1.
- la valeur de F est 0,5 N, que deviennent
- l'énergie mécanique ?
- la vitesse en B et D ?
|
 |
corrigé |
| altitude de B
hB =AB sin(b)= 0,3973 m
altitude de D
hD= hB+OD(1+ cos(a))= 2,275 m
énergie mécanique en A
sous forme d'énergie cinétique
0,5 mvA²
danger!!!! vitesse en m s-1
0,2 J
énergie mécanique en B
0,5 mvA²+F*AB= 4,2 J
|
|
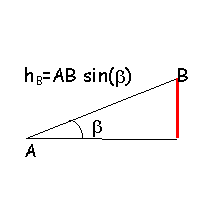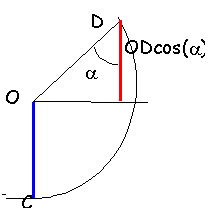 |
vitesse en C = vitesse en B (aucune force ne travaille entre B et C )
énergie mécanique en C: 4,2 J
énergie potentielle en C: 0,1*9,8*0,3973 = 0,389 J
énergie cinétique en C: 3,811 J
vitesse en C: rac carrée (3,811 *2 / 0, 1)
8,73 m s-1 = 8,73*3,6=31,43 km h-1. énergie mécanique en D: 4,2 J
énergie potentielle en D: 0,1*9,8*2,275 = 2,23 J
énergie cinétique en D: 1,97 J
vitesse en D: rac carrée (1,97*2 / 0, 1)
6,28 m s-1 = 6,28*3,6=22,6 km h-1.
l'énergie mécanique vaut :
1,2 J
vitesse en B
1,2 = 0,5mvB²+ mg altitude B
1,2 = 0,5mvB²+0,1*9,8*0,3973= 4 m s-1 En D l'énergie mécanique vaut :
1,2 J
vitesse en D
1,2 = 0,5mvD²+ mg altitude D
1,2 = 0,5mvB²+0,1*9,8*2,275
le calcul conduit à une valeur négative pour 0,5mvB² ; D ne peut être atteint
En B
|
|
| exercice 5 |
énergie, puissance, frottements |
Pour faire rouler une voiture pendant une minute,à la vitesse constante 90km/h,son moteur reçoit une énergie de 4,8 MJ qui provient de la combustion de l'essence. Le rendement du moteur est de 30%. La combustion d'un litre d'essence fournit 35 MJ. La route est horizontale.
- Calculer l'énergie mécanique fournie par le moteur considéré pendant une minute. En déduire la puissance mécanique moyenne.
- Calculer la valeur des forces de frottements supposées constantes.
- Quelle sera la consommation pour parcourir 100 km à la vitesse indiquée.
corrigé |
| énergie mécanique : 4,8*0,3 = 1,44 106 J
puissance (watt) = énergie mécanique (joule) / durée (seconde)
P = 1,44 106 / 60 = 24 kW La puissance mécanique mise en jeu est utilisée pour compenser la puissance perdue lors des frottements avec la route . Force motrice et force de frottements sont opposées.
puissance (watt) = force motrice (N) * vitesse (ms-1).
vitesse =90/3,6=25 ms-1....F = 24 000 / 25 = 960 N. consommation à chaque minute : 4,8 / 35 = 0,137 L
en 60 s on parcourt 60*25 = 1500 m
consommation aux 100 km: 0,137*100/1,5 = 9,13 L
|
|
|
|
|
|
| exercice 6 |
looping |
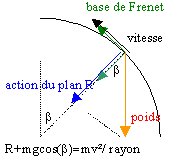
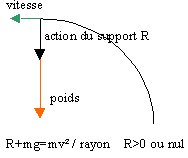
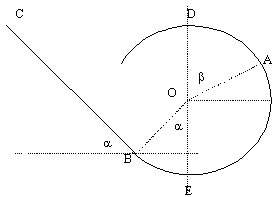
| Un solide de masse m se déplace dans une glissière constituée d’une partie rectiligne BC suivie d’une partie circulaire de centre O et de rayon R. Les frottements sont négligés. g=10 ms-2. L’origine des altitudes est le point B. Le solide est lâché de C sans vitesse. |
|
1. Représenter en B et en A les forces appliquées au solide et le vecteur vitesse
2. Exprimer l'énergie mécanique en A et C, puis la vitesse en A en fonction des données
q Calculer la vitesse en A si m=100g R=0,5m BC=2m
a =1,2 rad ; a =1rad
3. La vitesse minimale en D doit être supérieure à racine carrée (10*R) sinon le point D n'est pas atteint. Quelle doit être l'énergie minimale en C permettant d'atteindre D. En déduire l'altitude minimale de C permettant d'atteindre D.
|
|
| Répondre par Vrai ou Faux .Justifier.
1 .En E la somme des forces est nulle.
2 .Si la masse quadruple, la vitesse en A double.
3 .Si le rayon quadruple, la vitesse en A double.
4 .Si la vitesse réelle en A est la moitié de celle calculée, alors 50% de l 'énergie est dissipée sous forme de chaleur lors des frottements
corrigé
l'énergie mécanique se conserve
Va²=2g(BC sin(a)-OB(cos(a)+cos(b)))
- vitesse en A : 5,3 ms-1
- énergie minimale permettant d'atteindre D
- mgOB(cos(a)+1)+0,5 m Vd2 avec Vd2=gOB
- 0,93 J
tout est faux
- au point E la vitesse n'est ni constante, ni nulle : donc la somme des forces n'est pas nulle
- dans l'expression de la vitesse la masse ne figure pas
- la vitesse n'est pas proportionnelle à la racine carrée du rayon OB
- seule l'énergie cinétique est divisée par 4 alors que l'énergie potentielle ne change pas
|
|
| exercice 1 |
énergie mécanique d'un oscillateur élastique
|
|
A l'instant t=0, le centre d'inertie d'un oscillateur élastique non amorti, de masse m=200g et de constante de raideur k=50Nm-1, a pour abscisse x0=0 (sa position d'équilibre). Il est animé d'une vitesse 2 ms-1. L'énergie mécanique de cet oscillateur est de : 1 J ; 0,2 J ; 20 mJ ; 2kJ ; 0,4 J (choisir la bonne réponse)
|
|
..
|
| corrigé |
|
|
| L'énergie potentielle élastique de l'oscillateur est nulle au passage à la position d'équilibre. Toute l'énergie mécanique est sous forme cinétique. m=0,2 kg ;
0,5 mv2=0,5*0,2*4=0,4 J
|
|
|
| exercice2 |
mouvement circulaire uniforme
|
|
Deux ciyclistes A et B se déplacent dans le même sens sur une piste circulaire. Ils tournent à des fréquences constantes (1,25 tours / min pour A et 1 tour / min pour B). A la date t=0, prise comme origine de l'étude, leurs positions sont diamètralement opposées. La date t (minutes) à laquelle A rattrape B pour la première fois est : 1 ; 3 ; 2 ; 4 ; 0,5 .
|
|
..
|
| corrigé |
|
|
| Le cycliste A possède 0,5 tour de retard et à chaque minute il éffectue 0,25 tour de plus que B
Le retard est rattrapé en 2 minutes
|
|
|
|
|
| exercice 3 |
action du plan incliné
|
|
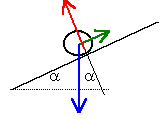
Un solide de poids P=3,6 N peut glisser sans frottement, selon la ligne de plus grande pente, sur un plan incliné de 30° par rapport à l'horizontale. Il est maintenu en équilibre grâce à un fil de direction parallèle au plan et attaché à un support fixe. La valeur de la tension exercée par le fil sur le solide est :..3,6N ; 1,8 N ; 3,1 N ; 9,8 N ; 7,2 N
|
|
..
|
| corrigé |
|
|
 |
|
action plan
P cos(c)
3,1 N
|
tension du fil
P sin(a)
1,8 N.
|
|
|
| exercice 4 |
équilibre d'un solide soumis à 4 forces
|
|
Une pédale de poids P=4 N, de longueur OA, est mobile autour d'un axe passant par O, perpendiculaire au plan de la figure. On exerce en A une force horizontale F=30 N. La pédale est en équilibre quand le fil CD (OC=0,75 OA) est tel que : l'angle a =30° et DC perpendiculaire à OA.
La valeur de la tension T est : 15N ; 32,8 N ; 4 N ;31,7 N ; 22,3 N.
|
|
.
|
| corrigé |
|
|
|
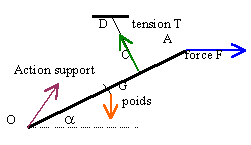
P OG cos(a)+F OA sin(a)-T OC=0
P *0,5 cos(a)+F OA sin(a)-T* 0,75=0
T=22,3 N
|
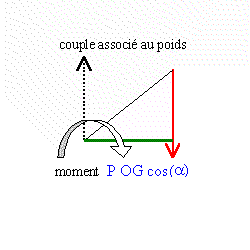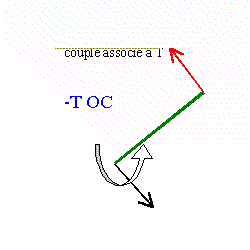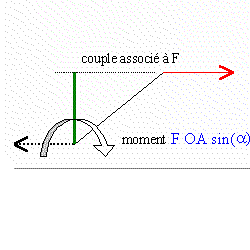 |
|
|
| exercice 5 |
puissance mécanique rendement énergie
|
|
Une voiture se déplace, en ligne droite, à la vitesse constante de valeur 100 kmh-1. La puissance mécanique disponible sur l'arbre moteur est 15 kW. Le rendement global du moteur est de 35%. Un litre d'essence libère 3,35 107 J. La consommation en litres aux 100 km est:4,6 ; 9,2 ; 7,4 ; 13,8 ;8,4
|
|
..
|
| corrigé |
|
|
| Energie mécanique mise en jeu chaque seconde 15000 J soit par heure 5,4 10 7 J.
Energie utile fournie par litre d'essence 0,35* 3,35 107 =1,172 107 J
consommation aux 100 km:4,6 L
|
|
|
| exercice 6 |
calorimètre : Quelle masse d'eau est congelée ?
|
|
Dans un calorimètre de capacité calorifique négligeable, on introduit une masse d'eau égale à 300g. la température d'équilibre de l'eau est 4°C. On introduit alors un bloc de fer de masse 200g à la température de -70°C. La masse d'eau congelée est égale à: 300g ; 4,25 g ; 100g ;10,2 g ; 42,5 g.
capacité thermique massique (J°C-1kg-1) eau: 4180 ;fer : 460 chaleur latente fusion de la glace 335kJkg-1
|
|
.
|
| corrigé |
|
|
| Hypothèse: le mélange contient de l'eau et de la glace (et du fer). La température finale d'un mélange eau glace est 0°C tant qu'il y a de l'eau et de la glace en présence.
énergie gagnée par le fer: masse (kg)*capacité thermique massique* diff. température
0,2*460*70=6440 J
énergie cédée par le liquide (eau ) passant de 4 à 0°C tout en restant liquide 0,3*4180*4=5016 J
énergie cédée par une partie du liquide qui gèle: 6440-5016=1424 J
masse d'eau qui gèle: 1414 / 335000=4,25 g
|
|
|
| exercice 7 |
sèche linge : évaporation de l'eau
|
|
Un sèche linge consomme une puissance électrique de 3500 W. Le séchage s'obtient par élévation de température de l'eau du linge jusqu'à 100°C puis vaporisation à 100°C. Le linge est initialement imprégné de 4 kg d'eau à 18°C. L'énergie nécessaire pour sécher totalement le linge humide est égale à: 3000J ;108 J ; 1,04 1010 J ; 1,37 10 6 J ;
capacité thermique massique (J°C-1kg-1) eau: 4180 ; chaleur latente vaporisation de l'eau 2261 kJ kg-1
|
|
.
|
| corrigé |
|
|
| énergie nécessaire à élever la température de 4 kg d'eau de 18 à 100°C, l'eau restant liquide
4*4180*(100-18)= 1,37 10 6 J
énergie nécessaire pour vaporiser 4 kg d'eau à 100°C: 4*2216 103=9,044 106 J
total: 10,41 10 6 J
|
|
|
| exercice 8 |
bilan énergétique d'un générateur électrochimique
|
|
L'énergie chimique emmagasinée dans un générateur électrochimique est de 24 kJ. Lors de la transformation en énergie électrique les pertes internes sont de 20%. Ce générateur alimente un conducteur ohmique de résistance 6 W et se décharge en 2 minutes.En supposant que l'intensité reste constante , sa valeur est égale à: 5,78 A ; 2,58 A ; 5,16 A ; 10 A ; 6 A.
|
|
..
|
| corrigé |
|
|
| énergie électrique disponible aux bornes du générateur : 24*0,8 =19200 J
E (J) =R (W) * I2 (A) * temps (s)
19200=6*I2*60*2 ........l'intensité est : 5,16 A
|
|
|
| exercice 9 |
chaîne énergétique : moteur pompe
|
|
Un petit moteur électrique est alimenté sous une tension de 110 V. Il actionne une pompe qui élève l'eau d'un puit à une hauteur de 7,5 m et dont le débit est de 56 L à la minute. La puissance mécanique de la pompe est de 70 W ; 4200 W ; 7 W ; 70000 W ; 700 W
g=10 ms-2 ; masse volumique de l'eau 1000 kgm-3.
|
|
.
|
| corrigé |
|
|
| masse d'eau pompée à chaque seconde : 56/ 60 = 0,933 kg s-1.
cette masse d'eau s'élève de 7,5 m
énergie mise en jeu à chaque seconde : mgh=0,933*10**7,5 = 70 Js-1 ou 70 W
|
|
|
| exercice 10 |
période radioactive
|
|
Le bismuth Bi (Z=83 A=212) est radioactif, émetteur a. Le noyau fils émis est du thallium. La période radioactive du bismuth est 60 minutes. La masse initiale de bismuth est 0,2 g. La masse de bismuth restant au bout de 3 heures est égale à : 0,178 g ; 0,141 g ; 25 mg ; 0,1 g ; 50 mg
|
|
..
|
| corrigé |
|
|
| Au bout de 1 heure ( une période) la masse de bismuth est divisée par 2
Au bout de 2 heures ( 2 périodes) la masse de bismuth est divisée par 22
Au bout de 3 heures ( 3 périodes) la masse de bismuth est divisée par 23
0,2 divisé par 8 =25 mg
|
|
|
| exercice 11 |
réactions nucléaires : durée de vie du soleil
|
|
Les réactions nucléaires qui se produisent dans le soleil libèrent une énergie voisine de 3,46,1031 J par jour. La masse du soleil est évaluée à 2 1030 kg. En années, la durée de vie probable du soleil est égale à :5 109 ;
1,42 1013 ; 5,2 1015 ; 47 510 ; 25 000.
vitesse de la lumière 300 000 kms-1 une année =365 jour
|
|
..
|
| corrigé |
|
|
| E=mc2
la masse du soleil diminue chaque jour du fait des réactions nucléaires de :
3,46 10 31 / 9 1016 =3,844 1014 kg
perte de masse en un an 1,4 1017 kg
durée de vie probable : 1,42 1013
|
|
|
| exercice 12 |
fission de l'uranium dans un réacteur nucléaire
|
|
Dans un réacteur nucléaire, l'énergie est produite par la fission de l'uranium 235. Lors de la fission d'un atome d'uranium 235 la perte de masse vaut 4,45 10-3 u. L'énergie libérée par la fission de 1 kg d'uranium 235 est égale à : 5 109 J ; 1,7 109 J ; 5,2 1015 J ; 1029 j ; 1,7 1012 J
1 u= 1,66 10-27 kg. vitesse de la lumière c=3 108ms-1 ; nombre d'Avogadro 6,02 1023 mol-1 masse molaire de l'uranium 235 g mol -1
|
|
..
|
| corrigé |
|
|
| perte de masse lors de la fission d'un atome 4,45 10-3 *1,66 10-27 =7,387 10-30 kg
perte de masse lors de la fission d'une mole d'atomes 7,387 10-30 *6,02 1023 =4,46 10-6 kg pour 0,235 kg de métal.
perte de masse lors de la fission d'un kg 4,46 10-6 / 0,235 = 1,89 10-5 kg
E=mc2
énergie libérée : 1,89 10-5 *9 1016 =1,7 10 12 J
|
|
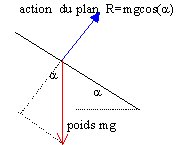
Un skieur de masse m=90,0 kg descend une piste inclinée d'un angle de 14° sur l'horizontale à une vitesse constante de 70,0 km/h. Les forces de frottement de la piste sur les skis ainsi que celles de l'air ont une résultante F parallèle à la pente.
- Faire l'inventaire des forces agissant sur le skieur.
- Le principe d'inertie permet de calculer la valeur de F. Pourquoi ? Calculer F.
- Quel est le travail de cette force lorsque le skieur parcourt une distance de 100 m dans ces conditions ?
- Quelle est la puissance de F ?
- Quel est le travail du poids du skieur pour ce même parcours ?
corrigé
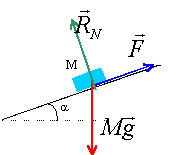
d'après le principe d'inertie, le mouvement du skieur étant rectiligne uniforme, ce dernier est pseudo-isolé ( somme des vecteurs forces égale zéro).
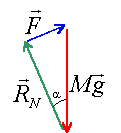
dans le triangle des forces : F= Mg sin a = 90*9,8*sin14 = 213,3 N.
travail de cette force :
vecteur force et vecteur déplacement colinéaires et de sens contraire
W = F * déplacement * cos 180 = - 213,3* 100 = - 21 330 J .
Puissance de cette force :
force de frottement et vitesse, vecteur colinéaires et de sens contraire
Puissance = F v cos 180
exprimer la vitesse en m/s : 70 /3,6 = 19,44 m/s.
puissance = -213,3*19,44 = -4146 W.
travail du poids :
La somme des forces est nulle, en conséquence la somme des travaux des forces est nulle.
Rn, perpendiculaire au sol ne travaille pas
le travail du poids est donc opposé au travail de la force F .
|
|
Pour préparer un sportif à une compétition de lancer de poids, (m=7,30 kg), on simule son geste ; voici les résultats obtenus en notant G le centre d'inertie de la boule.
Hauteur du point O où le poids quitte la main du lanceur : 1,90m.
Hauteur maximale atteinte par le poids : 4,50m à une distance de O égale à 6,72 m (point S).
Distance horizontale du lancer : 16,20m (point D).
Durée du lancer : 1,64 s.
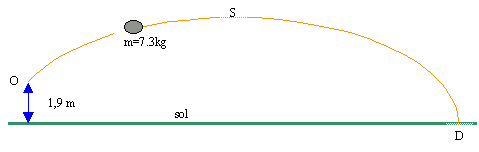
- Calculer le travail du poids au cours du déplacement de O jusqu'à D.
- On note par M un point quelconque de la trajectoire de G.
- Où sont situés les points M si le travail du poids W (P) de O à M est résistant ?
- Pour quel ensemble de points ce travail est-il moteur ?
- Pour chaque phase, la vitesse de G est-elle supérieure ou inférieure à la vitesse au moment du lâcher au point O ?
corrigé
Le travail d'une force constante ne dépend pas du chemin suivi, mais uniquement des positions initiale et finale :
Le référentiel est la surface de la terre.
travail du poids = mg( h départ - h fin)
l'origine des altitudes est prise à la surface du sol.
W = 7,3*9,8*(1,9-0) = 136 J.
entre les points O et S, le travail du poids est résistant (négatif) : l'altitude finale étant supérieure à l'altitude de départ.
la vitesse du poids est inférieure à la vitesse initiale en O.
entre les points S et D, le travail du poids est moteur (positif) : l'altitude finale étant inférieure à l'altitude de S.
la vitesse du poids est supérieure à la vitesse initiale en S, mais reste inférieure à la vitesse initiale tant que l'altitude dépasse 1,9 m.
la vitesse du poids est supérieure à la vitesse initiale en O ( entre S et D) lorsque l'altitude du poids est inférieure à 1,9 m.
|
|
un tapis roulant est utilisé pour charger du minerai dans un wagon.
La longueur du tapis est L = 22,5 m et son inclinaison avec l'horizontale est a = 35°
- Faire le bilan des forces s'exerçant sur un bloc de minerai de masse M = 2 kg qui est entraîné a vitesse constante sur le tapis roulant.
- Calculer la valeur de la force de frottement f exercée par le tapis roulant sur le bloc de minerai (expression littérale avant application numérique).
- Calculer le travail de cette force de frottement lorsque le bloc parcourt toute la longueur du tapis roulant.
- Quelle est la puissance des forces exercées par le tapis sur le minerai transporté si la vitesse de chargement du wagon est de 1,55 tonne par minute ?
corrigé
Le bloc de pierre est soumis à son poids et à l'action du tapis: celle ci peut être représentée par deux forces l'une f parrallèle au tapis et l'autre perpendiculaire au tapis
La vitesse est constante et le mouvement rectiligne alors la somme vectorielle des forces est nulle.
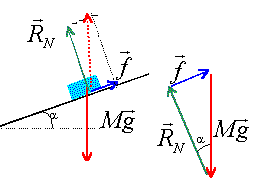
f = Mg sin 35 = 2*9,8 sin 35 = 11,2 N.
travail de cette force : force et déplacement sont colinéaires et de même sens
donc le travail est égal à : f L = 11,2*22,5 = 253 J.
vitesse de chargement : 1550 kg en 60 s soit 1550/60 = 25,8 kg / s
La puissance (watt) mise en jeu est le travail (J) effectué à chaque seconde.
253 J pour déplacer 2 kg.
on peut déplacer 25,8 kg / s donc :
P = 253*25,8 / 2 = 3264 watts.
|
|
Rotation et translation d'un cube homogène :
Un cube homogène, de masse m = 100 kg et d'arête a = 50 cm, peut être suspendu de deux facons.
Dans le schéma 1, il est suspendu à une tige rigide de longueur L = 1 m. Cette tige pivote autour d'un point O, mais est fixée rigidement au centre C de la surface supérieur du cube.
Dans le schéma 2, il est suspendu à deux cordes parallèles de même longueur L = 1 m. Ces cordes sont fixées en O1 et O2 sur la même horizontale et attachées au cube par les centres A1 et A2 des deux arêtes parallèles de sa face supérieure.
Au départ, la tige et les deux cordes sont verticales. On déplace le tout jusqu'à ce que la tige ou les cordes fassent un angle de 30° avec la verticale.
Déterminer le travail du poids du cube dans les deux cas.
corrigé
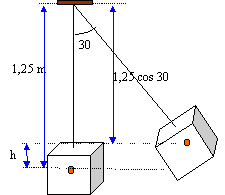
travail du poids lors du déplacement de la position verticale à la position oblique.
l'altitude du centre d'inertie du cube (position verticale) est prise comme origine des altitudes
W = mg (0- h)
avec h = 1,25 -1,25 cos 30 = 0,167 m
m =100 kg ; g = 9,8 N / kg
W = - 100*9,8*0,167 = -163,6 J.
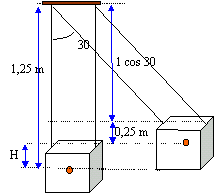
travail du poids lors du déplacement de la position verticale à la position oblique.
l'altitude du centre d'inertie du cube (position verticale) est prise comme origine des altitudes
W = mg (0- H)
avec H = 1,25 -(0,25 +1 cos 30) = 0,134 m
m =100 kg ; g = 9,8 N / kg
W = - 100*9,8*0,134 = -131,3 J.
|
|
Deux automobilistes A et B se déplacent sur une autoroute rectiligne. Les équations horaires de leurs mouvements sont XA (t) = 108 t + 27 XB (t) = - 126 t + 172 où XA et XB désignent les abscisses des 2 véhicules A et B comptées à partir de la même origine d'un repère d'espace et exprimées en km et t la date exprimée en heures.
- Quelle est la distance qui sépare les deux véhicules à t = 0
- Les 2 véhicules vont-ils dans le même sens ?
- A quelle date se croisent-ils ou se dépassent-ils ?
- Déterminer l'abscisse de croisement ou de dépassement.
- Au moment du dépassement ou du croisement quelle distance ont ils parcouru.
corrigé
|
|
|
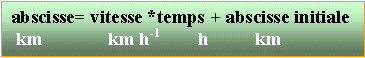
Un signe - devant la vitesse signifie que le véhicule B se déplace en sens contraire de l'axe.
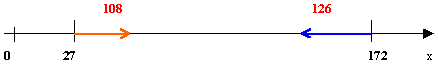
La distance séparant A et B à la date t=0 est 172-27 = 145 km.
Lors du croisement les abscisses de A et B sont identiques
108 t + 27 = -126 t +172
t =( 172-27) / (108+126) = 0,619 h ou 31 min 11 s
abscisse du croisement : remplacer le temps par la valeur précédente dans l'une ou l'autre espression de l'abscisse.
108*0,619 +27 = 93,85 km
distance parcourues :
par A : 93,85-27 = 66,85 km
par B : 172-93,85 = 78 ,15 km
|
| 2
relativité du mouvement
|
Au cours d'un vol entre Paris et Toulouse, un Airbus, volant à V1 = 820 km/h par rapport au sol, suit la voie ferrée du T.G.V (supposée rectiligne) , la vitesse de croisière d'un T.G.V (allant de Toulouse vers Paris ) est V2 = 320 km/h par rapport au sol .On supposera les portions rectilignes et on prendra un repère d'espace x'x orienté de Paris vers Toulouse
- Quelle est la vitesse d'un chef de gare assis à son bureau par rapport à un passager assis dans l'Airbus
- Quelle est la vitesse de l'Airbus par rapport à un passager assis dans le T.G.V?
- Lorsque l'Airbus et le T.G.V se croisent quelle est la vitesse d'un passager assis dans le TGV par rapport à l'Airbus ?
corrigé
|
|
|
Le référentiel est le sol.
Dans ce référentiel le chef de gare est immobile alors que l'avion se déplace vers Toulouse à la vitesse de 820 km/h.
Pour un passager de l'avion le chef de gare et la gare se déplace vers Paris à la vitesse de 820 km/h. Dans le référentiel lié au sol le train se déplace vers Paris à la vitesse de 320 km/h.
Pour un passager de l'avion, le train se déplace vers Paris à la vitesse de 820+320 km/h
Pour un passager du train, l'avion se déplace vers Toulouse à la vitesse de 820+320 km/h
|
| 3
système de poulies
|
Une poulie (P1) de rayon R1 = 300 mm entraîne par l'intermédiaire d'une courroie une poulie (P2) de rayon R2 = 100 mm . La poulie (P1) tourne à raison de n1 = 180 tours / mn.
- Déterminer sa fréquence de rotation.
- Déterminer sa période.
- Déterminer sa vitesse angulaire w1.
- Déterminer la vitesse linéaire d'un point de la périphérie de la poulie ?
- Quelle est la vitesse linéaire des points de la courroie ?
- En déduire la vitesse angulaire w2 de la poulie (P2) ?
corrigé
|
|
|
180 tours par minute soit 3 tours par seconde; fréquence = 3 Hz
période : durée pour éffectuer un tour = 1/3 = 0,33 s
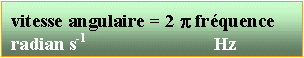
6,28*3 = 18,84 rad s-1.

18,84 * 0,3 = 5,65 m s-1.
Si la courroie ne patine pas, la vitesse d'un point de la courroie est 5,65 m s-1.
La poulie la plus petite tourne plus vite que la grosse. Le rapport des vitesses de rotation est l'inverse du rapport des diamètres.
le rapport de diamètres est 1/3. Donc
w2 = 3*w1 =56,5 rad s-1.
|
| 4
raideur d'un ressort
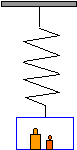
|
On considère deux ressorts à réponse linéaire, de longueur à vide lo = 30 cm, dont on veut déterminer expérimentalement les constantes de raideur k1 et k2.
- Faire l'inventaire des forces extérieures s'exerçant sur les 3 systèmes suivants
- Le plateau + les charges
- le ressort
- plateau + charges +ressort
- Donner un exemple de 2 forces liées entre elles par le principe des interactions
- Montrer la relation m .g = k . x on rappelle g = 9,8 N.kg-1
- On obtient expérimentalement les 2 graphes ci-dessous (allongement x (en m) en fonction de la masse m (en g)). Déterminer les coefficients directeurs des 2 graphes
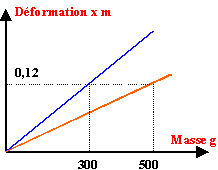
- En déduire les constantes de raideur k1 et k2 des 2 ressorts
- Déterminer la valeur de la masse m disposée sur le plateau lorsque la longueur du ressort n°2 (ressort ayant la plus grande raideur) est 37cm
- Quelles sont les longueurs respectives l1 et l2 des ressorts lorsqu'on exerce à l'extrémité de chacun une force F = 3,5N
corrigé
|
|
|
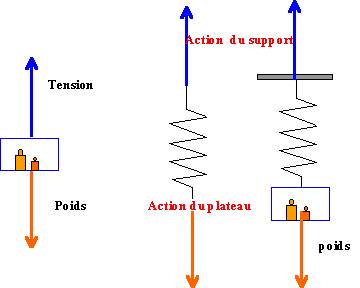
action du plateau sur le ressort et tension du ressort (ou action du ressort sur le plateau) sont liées par le principe des actions mutuelles.
A l'équilibre du plateau suspendu , le poids et la tension du ressort sont opposés
poids (N) = masse (kg) * 9,8
tension proportionnelle à l'augmentation de longueur du ressort (mètre) . La constante de proportionnalité est appelé raideur notée k en N /m.
mg = kx
coefficient directeur des droites :
0,12 /0,3 = 0,4 m kg-1.
0,12 /0,5 = 0,24 m kg-1.
raideur des ressorts (N m-1):
9,8 N/kg divisé par les valeurs précédentes (m /kg).
9,8 /0,4 = 24,5 N m-1.
9,8 /0,24 = 40,8 N m-1.
allongement du ressort : 37-30 = 7 cm = 0,07 m
tension : 40,8 *0,07 = 2,85 N
poids = m *9,8 = 2,85
m = 285 g
déformations des ressorts : tension / raideur
3,5 /24,5 = 0,143 m =14,3 cm --> longueur = 30+14,3 = 43,3 cm
3,5 /40,8 = 0,086 m =8,6 cm --> longueur 30+8,6 = 38,6 cm.
|
|
contre poids et poulie
|
Une brique B de masse 1 kg est entrainée a la vitesse constante sur une table horizontale par un contrepoids C de masse 0,2 kg . On prendra g=10 Kg.N-1. Les frottements sont supposés négligeables au niveau de la poulie et le fil est de masse negligeable et inextensible.
- Faire le bilan des forces qui s'exercent sur le contrepoids C. Calculer l'intensité de ces forces.
- Même question pour les forces qui s'exercent sur la brique B .Le contact entre la brique et la table est il avec ou sans frottement.
- Comment évolue le système (brique+contrepoids) en absence de frottements sur la table.
corrigé
|
|
|
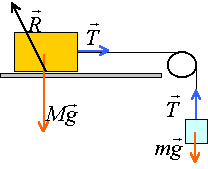
Le contre poids est pseudo isolé :
tension du fil opposé au poids du contre poids : norme 0,2*10 = 2N
La brique est soumise à son poids, à l'action du sol et à la tension du fil.
La vitesse est constante alors la somme des forces appliquées à la brique est nulle.
en conséquence le poids de la brique ne peut pas être opposée à l'action du sol : les frottements ne sont pas nul
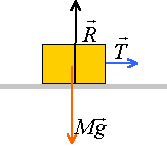
en l'absence de frottements sur la table la brique n'est pas pseudo isolée:
sa vitesse va croître jusqu'à ce que le contre poids touche le sol.
|
| 2
chute libre sans vitesse initiale
|
On lache sans vitesse initiale une premiere bille d'un point A situé a une hauteur de 2,20 m au dessus du sol ; 0.2 5s plus tard, on lache sans vitesse initiale unje seconde bille d'un point B situé à 2,70 m au dessus du sol . A et B sont 2 points situés sur une même trajectoire verticale. Les forces de frottements dues à l'air agissant sur les billes sont négligeables .
- Quelle est la vitesse de la premiere bille lorsquelle touche le sol et quelle est la durèe de la chute.
- Quelle est la vitesse de la seconde bille lorsque la premiere touche le sol et è quelle hauteur du soil se trouve t-elle a cet instant.
- Quelle est la vitesse moyenne de la 2éme bille lorsquelle frappe le sol.
corrigé
|
|
|
hauteur de chute :h=5 t²
vitesse v=10 t ou encore v²=20 h
bille n°1 : 2,2 = 5 t² donc t = 0,663 s et v= 6,63 m/s au sol
bille n°2 : durée de la chute 0,663-0,25 = 0,413 s donc v= 4,13 m/s
hauteur = 5 *0,413 ² = 0,853 m parcouru il en reste encore 2,7-0,853 = 1,847 m.
bille n°2 au sol : 2,7 = 5 t² d'où la durée de la chute t = 0,734 s ;
vitesse 10*0,734 =7,34 m/s
vitesse moyenne = distance (m) divisée par la durée du parcours (s)
2,7 / 0,734= 3,68 m /s.
|
| 3
ouvre boîte
|
Pour ouvrir une boite de conserve on tourne le papillon d'un ouvre boite. Pour cela on exerce 2 forces horizontales de valeur 5 N. Les forces sont appliquées sur le papillon qui est supposé vertical en 2 points distants de 4 cm .
- Montrer que l'on applique un couple de forces a l'appareil. Calculer le moment de ce couple de forces.
- Le papillon a tourné d'un angle a de 30 degrés. Les forces exercées sont toujours horizontales et ont la même valeur. Calculer le moment de ce couple .
corrigé
|
|
|
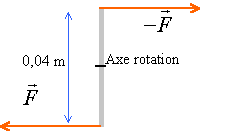
couple : 2 forces de direction parallèle, de sens contraire, de même norme
moment du couple 5*0,04 = 0,2 mN
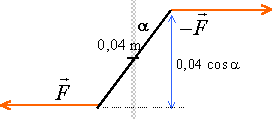
le papillon a tourné de 30 ° :
la distance n'est plus de 4 cm, mais plus petite 4 cos 30 =3,46 cm
moment du couple 5*0,0346 = 0,173 mN.
|
| 3
barrière
|
Une barrière de parking de masse M=60 kg est mobile autour d'un axe O. Cet axe est celui de l'arbre moteur servant à manoeuvrer la barrière. G centre de gravité de la barrière est situé à 20 cm à droite de O.
- La barrière est initialement horizontale, calculer le moment minimum du couple moteur pour la soulever.
- La barrière se soulève, lorsque la vitesse est constante, le moment du couple moteur est-il constant ?
- La barrière est inclinée de 80° sur l'horizontale; le moteur s'arrète et un couple de freinage maintient la barrière dans cette position. Calculer le moment de ce couple de freinage.
corrigé
|
|
|
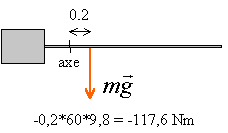
le moemnt du couple moteur compense (et dépasse légerement) le moment du couple associé au poids. M moteur = 117,6 Nm
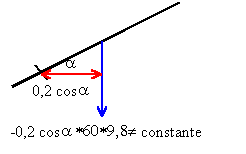
le moment du couple moteur diminue lorsque l'angle a augmente.
moment du couple de freinage
0,2 cos80 *60*9,8 = 20,4 Nm.
|
| exercice 1 |
chute verticale vers le bas |
|
Une bille de masse m=10g est lachée sans vitesse d'une hauteur de 50 m. Calculer :
- la vitesse atteinte et la distance parcourue à t=2s.
- la durée de la chute et la vitesse d'arrivée au sol.
- l'énergie potentielle initiale. (origine des altitudes : le sol)
- Si la masse double que deviennent les résultats précédents.
|
| corrigé |
|
| altitude initiale z0=50 m ; V0=0
à t=2 s : z=-4,9 *2² + 50 = 30,4 m ; distance parcourue : 19,6 m
vitesse algébrique=-9,8*2=-19,6 ms-1=-19,6*3,6 kmh-1
le signe moins signifie que le vecteur vitesse est dirigé vers le bas alors que l'axe des altitudes est dirigé vers le haut.
norme du vecteur vitesse : 19,6 ms-1.
arrivée au sol z=0 ; -4,9 t²+50=0 ; t =rac carrée(50/4,9 )= 3,19 s
norme de la vitesse = val absolue(-9,8*3,19) = 31,3 ms-1.
énergie potentielle de pesanteur = mgz =0,01*9,8*50 = 4,9 J
vitesse, durée et distance sont indépendantes de la masse
seule l'énergie potentielle double.
|
|
|
|
| exercice 2 |
chute libre verticale (plus dur) |
|
| La distance parcourue durant la dernière seconde de chute libre(sans vitesse initiale) est égale au quart de la distance totale de chute. Quelle est la hauteur de chute ?
Une bille est abandonnée sans vitesse initiale . Quelle est la distance parcourue pendant la neme secondes de chute ? g=10ms-2
|
| corrigé |
|
| distance parcourue = d = z0-z = 4,9 t² (t durée de la chute)
0,75 d= 4,9 (t-1)²
diviser membre à membre la seconde relation par la pemière :
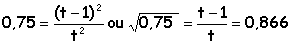
0,866 t=t-1 d'où t= 7,46 s.
distance parcourue d= 4,9*7,46²= 272,8 m t=1s alors x =5 m
t=2s alors x=20 m soit 15 m durant la 2éme seconde soit 5*(2n-1) avec n=2
t=3 s alors x=45 m soit 25 m surant la 3éme seconde soit 5*(2n-1) avec n=3
|
|
|
|
| exercice 3 |
lancer vertical de 2 balles |
Une première balle est lancée vers le haut avec une vitesse initiale de 8 ms-1 . Une seconde plus tard une autre balle est lancée vers le haut avec une vitesse initiale de 6 ms-1. Les deux balles partent du même endroit choisi comme origine.
- Quelle est l'altitude de la rencontre ?
|
corrigé |
| origine des temps : départ de la 1ère balle
balle n°1 : z = -4,9 t² + 8t
balle n°1 : z = -4,9 (t-1)² + 6(t-1)
La 1ère balle commence à redescendre lorsque la 2ème la rencontre.
-4,9 t² + 8t = -4,9 (t-1)² + 6(t-1)
développer t = 10,9 / 7,8 = 1,4 s.
altitude : -4,9 *1,4² + 8 *1,4 = 1,6 m
|
|
|
| exercice 4 |
profondeur du puits |
|
On lache une pierre sans vitesse du haut d'un puits. On entend "plouf" 3 s après le lacher.
Quelle est la profondeur du puits ? vitesse du son dans l'air 340 ms-1.
|
|
| corrigé |
|
| t1 durée de la chute et t2 durée de la remontée du son
d : profondeur du puits
t1 + t2 = 3 (1)
chute libre : d = 4,9 t1²
son : d = 340 t2
4,9 t1²= 340 t2 (2)
4,9t1²=340 (3-t1 ) développer et résoudre
t1= 2,88 s
profondeur 340*0,12 = 40,7 m
|
|
|
| exercice 5 |
parabole |
|
On lance un objet avec une vitesse initiale de 21,2 m/s dans une direction faisant un angle de 45° avec l'horizontale.
- S'il n'y avait pas de pesanteur, le principe d'inertie s'appliquerait. Quel serait alors le mouvement de l'objet? Repésenter les positions de l'objet au bout de 1, 2, 3 s. Echelle : 1cm pour 10 m.
- Sous l'action de la gravité, l'objet se retrouve plus bas que la trajectoire trouvée, d'une distance donnée par la loi de la chute libre. Placer les positions réellement atteintes au bout de 1, 2, 3 s.
- Au bout de combien de temps l'objet touche t-il le sol supposé horizontal?
- Peut-on en déduire la vitesse horizontale qu'il avait au moment du lancer? g=10 N /kg.
corrigé
absence de pesanteur:
le solide n'est soumis à aucune force ( solide isolé) alors le mouvement de
son centre d'inertie dans un référentiel galiléen est rectiligne
uniforme.( droite confondue avec la vitesse initiale inclinée de 45° sur l'horizontale)
distance (m) = 21,2 * temps en seconde.
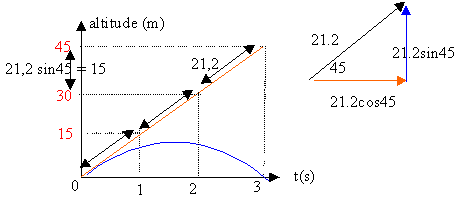
présence de la pesanteur :
( force verticale) seule la composante verticale de la vitesse est modifiée
alors que la composante horizontale de la vitesse reste inchangée.
loi de la chute libre avec vitesse initiale :
altitude (m) = -5 *temps ² +21,2 sin (45°) *temps (le temps est en seconde)
le signe moins vient du fait que dans le repère choisi l'axe des y est
vertical vers le haut alors que g ( gravité) est vertical vers le bas.
h = - 5t² +15 t
t = 1s : h = -5 +15 = 10 m
t= 2 s : h = -5*4 +30 = 10 m
t=3 s : h = -5 *3² + 45 = 0 m ( on est au sol)
ou bien plus simplement : écart entre la droite et la parabole : 5 t²
soit ( 5*1² ; 5*2²=20; 5*3²=45)
composante horizontale de la vitesse au moment du lancer :
à t =3 s l'objet est au sol
x = composante horizontale de la vitesse * temps
le mouvement suivant l'axe des abscisses est rectiligne uniforme car il n'y
a aucune force dirigée suivant l'horizontale
composnte horizontale de la vitesse : 21,2 cos45=15 m/s
|
| Circuits électriques :
Un aide de laboratoire doit réaliser le montage électrique suivant pour illustrer la loi des noeuds. D1, D2, D3 sont des dipôles à identifier ; A1, A2, A3 sont des ampèremètres.
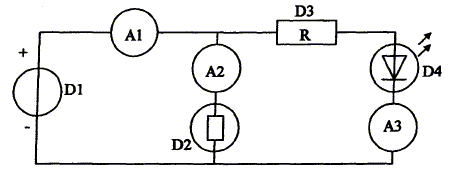
- Indiquer le sens conventionnel du courant dans chaque branche du circuit. Ajouter sur le schéma l'appareil de mesure permettant de mesurer la tension électrique aux bornes du dipôle D1.
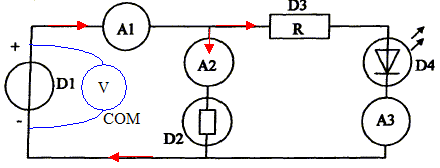
- Donner le nom de chaque dipôle.
D1 : générateur de tension continue ; D2 : lampe à incandescence ; D3 : résistor ; D4 : DEL
- L'ampèremètre A1 indique 172 mA et l'ampèremètre A3 20 mA. Quelle est la valeur indiquée par l'ampèremètre A2 ?
l'ampèremètre A2 indique : 172-20=152 mA
Sachant que la tension électrique mesurée aux bornes de D1 est 6,0 V, celle aux bornes de D4 de 1,8 V, quelle est la valeur de la tension électrique aux bornes des dipôles D2 et D3 ? La tension aux bornes des ampèremètres est nulle.
la tension électrique aux bornes des dipôles D2 : 6 V ; D3 : 6-1,8 = 4,2 V
En indiquant la loi utilisée, calculer la valeur de R. Préciser l'unité.
loi d'Ohm : R= U/I = 4,2 / 0,02 = 210 W.
Calculer la puissance électrique délivrée par le dipôle D1. Préciser l'unité.
U I = 6 *0,172 = 1,0 W
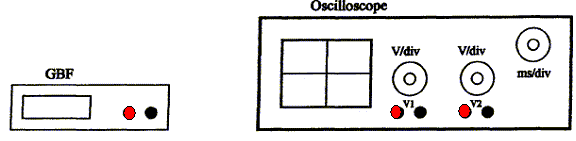
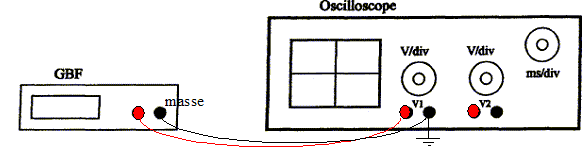
Indiquer sur le schéma ci-dessus les branchements à réaliser pour observer la tension électrique délivrée par le GBF en voie 1. Identifier la borne de masse et indiquer son symbole.
On observe l'oscillogramme ci-dessous sur l'écran de l'ozcilloscope. Représenter l'amplitude Um et la période T par des flèches et calculer leurs valeurs.
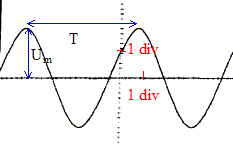
amplitude Um : 2 div soit 2*0,5 = 1 V ; T : environ 4,5 div soit 4,5*2 = 9 ms = 9 10-3 s.
Le fréquencemètre du GBF indique 0,110 kHz. Cette valeur est-elle en accord avec La valeur T précédente. Justifier par un calcul.
fréquence f = 110 Hz ; période T= 1/f = 1/110 = 9 10-3 s. ( accord)
On veut tester la tension électrique délivrée par un générateur de tensions basses fréquences ( GBF), en utilisant un oscilloscope. Les deux voies d'entrées sont réglées sur la même sensibilité 0,5 V/div et le balayage est fixé à 2ms/div.
|
électricité :
- Tension redressée : sur l'écran d'un oscilloscope on visualise l'oscillogramma ci-dessous ( 0,1 ms/div et 0,2 V/div)
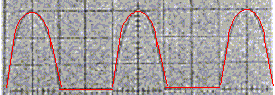
- Donner la liste du matériel nécessaire pour réaliser cette expérience.
générateur basse fréquence ou transformateur 220V / 6 V, oscilloscope, diode, résistor de protection de la diode
- Dessiner le schéma du montage :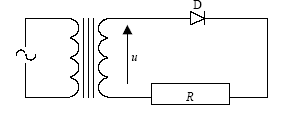
l'oscilloscope est monté en dérivation aux bornes du résistor R.
- Déterminer graphiquement la période, la fréquance et l'amplitude de cette tension.
période T : 4 div soit 0,4 ms = 4 10-4 s ; fréquence f= 1/T= 2500 Hz ; amplitude : 3 div soit 0,6 V.
- Quel composant faudrait-il changer dans le montage pour obtenir un redressement double alternance ? Donner son nom. Indiquer brièvement comment il est constitué.
la diode doit être remplacée par un pont redresseur de Graetz 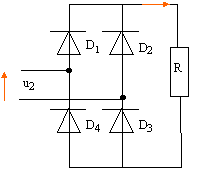
- Utilisation d'une lampe : une petite lampe porte sur son culot les indications suivantes : 6 V - 3 W
- Calculer l'intensité du courant électrique qui la traverse. P= UI soit I= P/U = 3/6 = 0,5 A
- En assimilant cette lampe à un conducteur ohmique, déterminer sa résistance dans les conditions de fonctionnement ci-dessus. Avec quel appareil pourrait-on vérifier le résultat trouvé ? Décrire la méthode utilisée.
U= RI soit R= U/I = 6/0,5 = 12 W ; ohmètre branché aux bornes de la lampe lorsque celle-ci ne fait pas partie d'un circuit traversé par un courant.
- Cette lampe est traversé par un courant de 0,25 A et la tension à ses bornes est 1,7 V. La lampe brille-t-elle normalement ? Pourquoi ?
puissance absorbée par la lampe ; 1,7*0,25 = 0,42 W ; la lampe brille très peu, elle ne fonctionne pas dans les conditions nominales ( 6V à ses bornes)
cocher les cases convenables du tableau suivant en précisant les caractéristiques des différents supports informatiques :
|
|
possibilité d'effacer des données |
capacité de stockage supérieure à 1 giga octets |
nécessité d'un lecteur spécifique |
peut transmettre un virus |
coût < 15 euros |
| disquette |
x |
|
x |
x |
x |
| disque dur de l'ordinateur |
x |
x |
|
x |
|
| CR-rom |
|
|
x |
x |
x |
| CR-rom réinscriptible |
x |
|
x |
x |
x |
| cartouche Zip |
x |
x |
x |
x |
x |
| disque dur USB amovible |
x |
x |
|
x |
|
|
| Circuits électriques :
Compléter le tableau suivant :
| nom |
symbole |
| lampe |
......... |
| ......... |
 |
| diode |
|
| ........ |
 |
Pour étudier un conducteur ohmique, on mesure simultanément l'intensité I qui le traverse et la tension U aux brnes, lorsqu'il est alimenté en courant continu. Quels appareils doit-on utiliser pour réaliser ces mesures ?
- Faire le schéma correspondant.
- Le constructeur précise la puissance maximale admissible P= 0,25 watt pour le conducteur ohmique de résistance R= 100 ohms. P= RI². Déterminer l'intensité maximale admissible pour ce conducteur.
réponse :
| nom |
symbole |
| lampe |
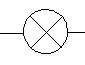 |
| transformateur |
 |
| diode |
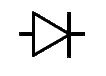 |
| pile |
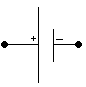 |
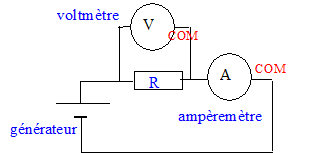
intensité maximale admissible pour ce conducteur : Imax = racine carrée (P/R )= racine carrée (0,25 / 100) =0,05 A.
Un transformateur porte l'indication : primaire 220 V / secondaire 6 V.
On alimente la bobine primaire avec une tension de 24 V. Indiquer la valeur de la tension lue au secondaire dans les deux cas suivants :
| primaire : 24 V alternatif |
primaire : 24 V continu |
| secondaire ...... |
secondaire .... |
Pourquoi est-il dangereux d'alimenter le secondaire du transformateur avec une tension alternative de 24 V ?
réponse :
rapport de transformation : 220/6 = 36,66
Le transformateur modifie la valeur efficace d'une tension alternative ; il ne sert à rien en courant continu.
| primaire : 24 V alternatif |
primaire : 24 V continu |
| secondaire : 24/36,66 = 0,65 V |
secondaire : zéro |
Il dangereux d'alimenter le secondaire du transformateur avec une tension alternative de 24 V car la tension primaire est très élevée : 24*36,66 = 880 V
Risques très importants d'électrocution.
|
|
|
Chers élèves voici le site dont tout un chacun recherchait !
Vous l'avait beaucoups recherché?
Alors des élèves du pays l'ont realisé pour vous !
vous pouvez aussi proposer des exercices
en ajoutant des commentaires
salut et bonne visite |
 |
Vous pouvez donner votre opinion sur des exercices
enfin d'y apporter des solutions. |
 |
Vous pouvez aussi proposer des exercices
pour l'enrechissement du site et pour nous permettre
de bien satisfaire les demandes et besoins des élèves. |
 |
Ce site est le premier site d'exercices totalement gratuit au senegal . |
 |
Il a été créé en 2008 par des élèves en classe de 1ère au lycée des parcelles assainies(LPA). |

|