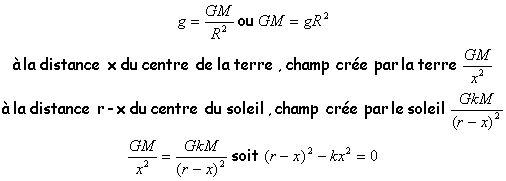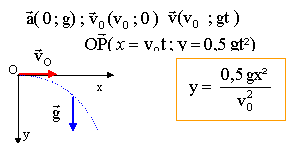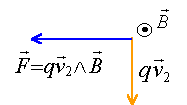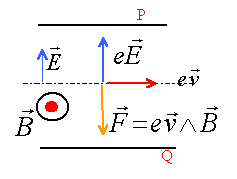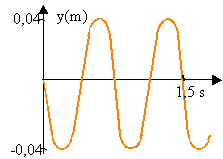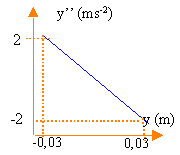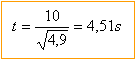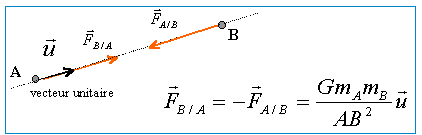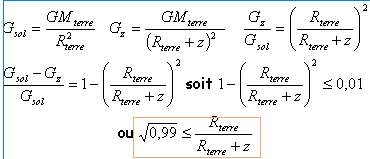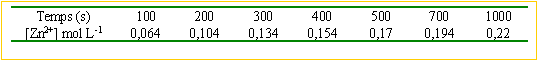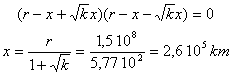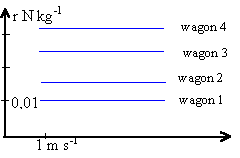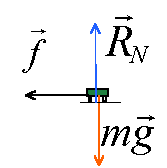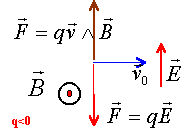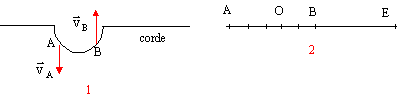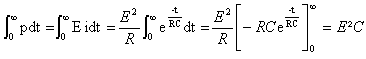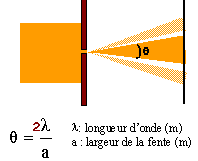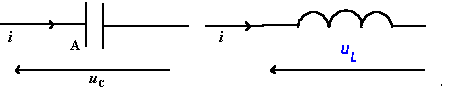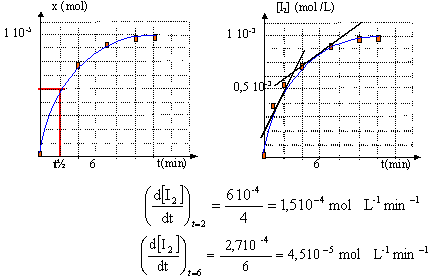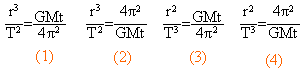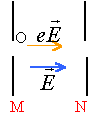exercices de terminale et des sujets de bac
La Galiote : trajectoire, chute libre, lois de Newton, électrolyse bac S 2007 France
La galiote était un navire de guerre qui fit son apparition à la fin du XVIIème siècle, sous le règne de Louis XIV. Les galiotes possédaient de lourds canons, fixés au pont, projetant des boulets de 200 livres (environ 100 kg) portant jusqu'à 1200 toises (environ 2400 m). Selon la description détaillée de Renau, Inspecteur Général de la Marine, ces bâtiments sont destinés à emporter des canons en mer. Ils sont de moyenne grandeur et à fond plat. De par leur fabrication, l'angle de tir des canons est fixe et a pour valeur a = 45°, ce qui permet de tirer à la plus grande distance possible. La structure d'une galiote doit être très robuste pour résister à la réaction considérable du boulet et leur échantillon* est ordinairement aussi fort que celui d'un vaisseau de 50 canons. * dimension et épaisseur des pièces utilisées pour la construction.
D'après le site Internet de l'Institut de Stratégie Comparée.
Les parties 1, 2 et 3 de cet exercice sont indépendantes.
Certaines aides au calcul peuvent comporter des résultats ne correspondant pas au calcul à effectuer.
Action de la poudre de canon sur le boulet :
L'éjection du boulet est provoquée par la combustion de la poudre. Une force de poussée est donc exercée sur le boulet par l'ensemble {galiote + canon + gaz}. Justifier l'expression soulignée dans le texte ci-dessus, à l'aide d'une des trois lois de Newton. Enoncer cette loi. (On pourra s'aider d'un schéma).
La trajectoire du boulet :
On souhaite étudier la trajectoire du centre d'inertie G du boulet de masse m. L'étude est faite dans le référentiel terrestre considéré comme galiléen. Le repère d'étude est (O,i , j ) et l'origine des dates est choisie à l'instant où le boulet part du point O.
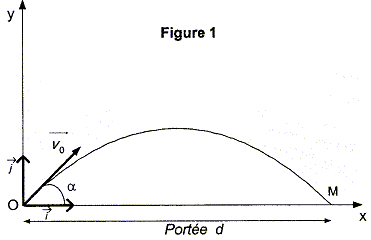
Le vecteur vitesse initiale v0 du point G est incliné d'un angle a (appelé angle de tir) par rapport à l'horizontale. Une fois le boulet lancé, la force de poussée de la partie précédente n'intervient plus. Volume du boulet : V = 16 dm3 = 16 L ; masse du boulet : m = 100 kg ; valeur du champ de pesanteur : g = 10 m.s-2 ; masse volumique de l'air : rair = 1,3 kg.m-3.
Aide aux calculs : 1,6*1,3 = 2,1 ; 2,4½ =1,5 ; 1,6/1,3 =1,2 ; 1,3/1,6 =0,81 ; 24½=4,9.
Inventaire des forces agissant sur le boulet après son lancement :
La poussée d'Archimède : donner l'expression littérale de la valeur FA de la poussée d'Archimède puis la calculer.
Le poids : calculer la valeur P du poids du boulet après avoir précisé son expression littérale.
Dans cet exercice, on pourra négliger la poussée d'Archimède devant le poids si la valeur de ce dernier est au moins cent fois plus grande que celle de la poussée d'Archimède. Montrer que l'on est dans cette situation.
Pendant le vol, compte tenu de la masse, de la vitesse et de la forme du boulet, on fait l'hypothèse que les forces de frottement dans l'air sont négligeables devant le poids. En tenant compte de la remarque et des résultats précédents, établir le bilan des forces exercées sur le système {boulet} pendant le vol.
Action de la poudre de canon sur le boulet :
Action : une force de poussée est donc exercée sur le boulet par l'ensemble {galiote + canon + gaz}.
Réaction : le boulet exerce une force opposée sur l'ensemble {galiote + canon + gaz}. Le canon recule s'il n'est pas solidement arrimé.
Enoncé de la 3è loi de Newton ou principe des action réciproques :
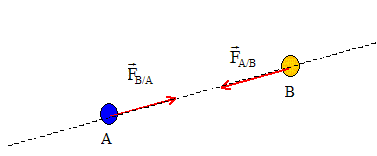
Interaction entre un objet A et un objet B : si un solide noté A exerce sur un solide noté B une force notée F A / B, alors B exerce sur A une force notée F B / A . Les deux forces associées à une même interaction sont toujours égales et opposées.
Inventaire des forces agissant sur le boulet après son lancement :
Expression littérale de la valeur FA de la poussée d'Archimède et calcul :
La poussée d'Archimède est égale au poids du volume de fluide ( dans ce cas, l'air) déplacé :
FA = V rair g avec rair = 1,3 kg.m-3; V = 16 L = 0,016 m3 ; g = 10 m/s².
FA = 1,3*0,016*10 = 1,3*0,16 = 0,21 N.
Valeur P du poids du boulet après avoir précisé son expression littérale :
P= mg avec m = 100 kg ; g = 10 m/s².
P = 100*10 = 1,0 103 N.
Le poids est environ 5000 fois plus grand que la poussée d'Archimède : celle-ci est donc négligeable devant le poids.
Pendant le vol, compte tenu de la masse, de la vitesse et de la forme du boulet, on fait l'hypothèse que les forces de frottement dans l'air sont négligeables devant le poids. En tenant compte de la remarque et des résultats précédents.
Bilan des forces exercées sur le système {boulet} pendant le vol.
Le boulet n'est soumis qu'à son poids ; le boulet est en chute libre.
Equation de la trajectoire :
Dans toute cette partie, on négligera la poussée d'Archimède et on ne tiendra pas compte des forces de frottement dues à l'air.
En appliquant la deuxième loi de Newton, montrer que les équations horaires du mouvement du point G s'écrivent :
x(t) =v0 cos a t ; et z(t) = -½g t2 + v0 sin a t
Montrer que l'équation de la trajectoire du boulet peut se mettre sous la forme y(x) = Ax2 + Bx. On donnera les expressions littérales de A et B et on précisera leurs unités respectives.
Portée du tir :
L'équation de la trajectoire du boulet peut se mettre sous la forme z(x) = x (Ax + B).
Au cours d'un tir d'entraînement, un boulet tombe dans l'eau. Dans ces conditions, la distance entre le point de départ du boulet et son point M d'impact sur l'eau est appelée portée). On négligera la différence d'altitude entre les points O et M devant les autres distances.
Exprimer le portée d du tir en fonction de A et B.
L'expression littérale de la portée d en fonction de v0, a et g est : d = v02 sin (2a) / g.
Retrouver, en la justifiant, la valeur a = 45° donnée dans le texte, pour laquelle la portée est maximale, pour une vitesse donnée.
A partir de la question précédente et des données, calculer la vitesse initiale du boulet pour atteindre la portée maximale donnée dans le texte.
En fait, les frottements dans l'air ne sont pas négligeables. Avec un angle de tir restant égal à 45°, la vitesse initiale du boulet doit-elle être supérieure ou inférieure à celle trouvée pour obtenir la même portée maximale ? Justifier sans calcul.
Equations horaires du mouvement du point G :
Ecrire la seconde loi de Newton appliquée au boulet :
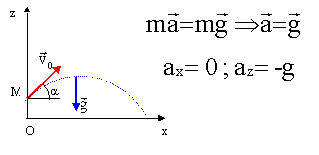
Coordonnées de la vitesse initiale : v0x = v0 cos a ; v0z =v0 sin a.
Le vecteur vitesse est une primitive du vecteur accélération :
vx(t) = v0 cos a ; vz(t) = -gt + v0 sin a.
Le vecteur position est une primitive du vecteur vitesse :
x(t) = v0 cos a t (1)
z(t) = -½gt2 + v0 sin a t (2)
x(t) =v0 cos a t ; et z(t) = -½g t2 + v0 sin a t
Equation de la trajectoire du projectile :
(1) donne t = x / v0 cos a. Repport dans (2).
z = -½ g x2/ ( v0 cos a)2 + x tan a.
Expression de la forme y(x) = Ax2 + Bx, avec A= -½ g / ( v0 cos a)2 et B= tan a
B est sans dimension ; A x2 a la dimension d'un longueur : x2 est une longueur au carré, donc A est l'inverse d'une longueur soit [A]= L-1.
Portée du tir :
L'équation de la trajectoire du boulet peut se mettre sous la forme z(x) = x (Ax + B).
Ecrire que l'altitude du boulet est nulle soit z= 0 d'où x=0 ( origine du tir) et x=d= -B/A.
L'expression littérale de la portée d en fonction de v0, a et g est : d = v02 sin (2a) / g.
La portée est maximale, pour une vitesse donnée si sin (2a) = 1 soit 2a = 90° , a =45°.
Vitesse initiale du boulet pour atteindre la portée maximale donnée dans le texte : d= 2400 m
d = v02 sin (2a) / g donne v02 = d g / sin (2a) avec sin (2a) = 1
v0 = (dg)½ ; v0 =(2400*10)½ = 2,4½*100 = 1,5 102 m/s.
En fait, les frottements dans l'air ne sont pas négligeables. Avec un angle de tir restant égal à 45°, la vitesse initiale du boulet doit être supérieure à celle trouvée pour obtenir la même portée maximale. Une partie de l'énergie mécanique du boulet est perdue soue forme d'énergie thermique lors des frottements sur les couches d'air.
:
Restauration d'un boulet par électrolyse
Un boulet est retrouvé par un archéologue, qui le restaure par électrolyse en solution basique. Ce procédé a pour but, notamment :
- d'éliminer la gangue (substance qui forme une enveloppe autour d'une autre matière) qui entoure le boulet ;
- de débarrasser l'objet de tous les ions chlorure qui, au contact de l'humidité de l'air et du dioxygène amènent à la formation d'acide chlorhydrique conduisant à la destruction rapide du boulet. Ces ions chlorure sont également présents dans la gangue.
Le schéma de principe de l'électrolyse est le suivant :
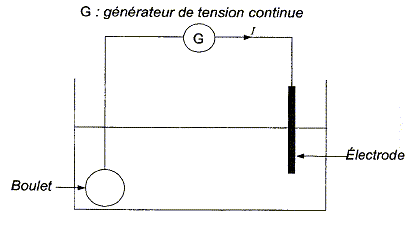
La lente destruction de la gangue libère dans l'électrolyse les ions chlorure qu'elle contenait. L'équation de la réaction modélisant l'électrolyse est :
2 Cl-(aq) + 2 H2O (l) = Cl2(g) + H2(g) + 2 HO-(aq)
Les couples d'oxydoréduction mis en jeu sont : Cl2(g) / Cl-(aq) et H2O(l) / H2(g)
La réaction se produisant à l'anode est-elle une oxydation ou une réduction ?
Ecrire l'équation de la réaction ayant lieu à l'anode. A quelle borne du générateur est reliée cette électrode ?
A l'une des électrodes, on observe un dégagement de dihydrogène. L'équation de la réaction électrochimique associée est :
2 H2O(l) + 2 e- = H2(g) + 2 HO-(aq) (1)
La pression exercée par le dihydrogène permet de décoller la gangue. L'élimination de la gangue se fait sous une intensité I constante et pendant une durée Dt qui dépendent, entre autre, de la nature de l'objet et de son état de corrosion. Charge élémentaire : e = 1,6 10-19 C ; constante d'Avogadro : NA = 6,0 1023 mol-1 ;intensité du courant : I = 1,0 A ; durée de l'électrolyse : Dt = 530 heures.
On note Q la valeur absolue de la charge électrique totale ayant circulé dans le dispositif pendant la durée D t de l'électrolyse.
Donner l'expression littérale du nombre N d'électrons transférés et celle de la quantité d'électrons n(e-) en fonction des grandeurs données.
Pour simplifier, on fait l'hypothèse que la réaction correspondant à l'équation (1) est la seule à se produire au niveau de l'électrode concernée.
En s'aidant éventuellement d'un tableau d'avancement, établir une relation entre la quantité n(H2) de dihydrogène dégagé et la quantité d'électrons n(e-) et en déduire que n(H2) =½ IDt/ ( eNA) . Calculer la valeur de n(H2).
En déduire quel sera le volume de dihydrogène dégagé dans les conditions de l'expérience. On donne le volume molaire des gaz dans les conditions de l'expérience : Vm = 24 L mol-1.
Aide aux calculs : 5,3*3,6 = 19 ; 2*1,6*6 = 19 ; 5,3/3,6=1,5 ; 2*6/1,6 = 7,5.
A l'anode positive, reliée à la borne positive du générateur, une oxydation a lieu : un réducteur libère des électrons.
Couple oxydant /réducteur Cl2(g) / Cl-(aq) : 2Cl-(aq) = Cl2(g) + 2e-.
Expression littérale du nombre N d'électrons transférés :
Une quantité d'électricité s'exprime par Q= I Dt ( en coulomb si I est en ampère et D t en seconde).
La valeur absolue de la charge d'un électron est e = 1,6 10-19 C.
d'où N e = I Dt ; N = I Dt / e.
Expression littérale de la quantité d'électrons n(e-) :
Dans une mole d'électrons, il y a NA électrons d'où : n(e-) = N/NA ; n(e-) = I Dt / (eNA).
Relation entre la quantité n(H2) de dihydrogène dégagé et la quantité d'électrons n(e-) :
2 H2O(l) + 2 e- = H2(g) + 2 HO-(aq)
D'après les coefficients stoechiométriques : n(e-) = 2 n(H2) ; n(H2) =½n(e-)
n(H2) = ½ I Dt / (eNA).
Volume de dihydrogène dégagé :
Volume d'un gaz (L) = quantité de matière (mol) * volume molaire des gaz ( L/mol)
V= n(H2) Vm = I Dt Vm / (2eNA).
avec Dt = 530*3600= 5,3*3,6 105 = 19 105 s ; I= 1,0 A ; Vm = 24 L/mol ; e = 1,6 10-19 C ; NA = 6,0 1023 mol-1.
eNA =1,6 10-19 * 6,0 1023 = 1,6*6 104.
V = 19 105 *24 / (2*1,6*6 104) = 19*24 *10 / (2* 1,6*6)
V = 19*24*10 / 19 = 2,4 102 L.
concours kiné C.E.E.R.R.F 03
| mongolfière
n néglige les frottements ; g=10m/s²
A- Une mongolfière se déplace verticalement dans l'air. La masse de l'ensemble {aérostier, mongolfière} a une masse initiale m1 et un volume V supposé constant.
- Donner la direction, le sens et l'expression de la valeur de la poussée d'Archimède F.
- Le mouvement de la mongolfière est decendant et accéléré ; on note a la valeur de l'acélération de l'ensemble ( a<g). Appliquer dans le référentiel terrestre supposé galiléen la seconde loi de Newton au système et projeter la relation obtenue sur un axe vertical orienté vers le bas.
- L'aérostier lâche du lest. Le mouvement de la mongolfière est maintenant accéléré vers le haut avec une accélération de même valeur a. La masse de l'ensemble est maintenant m2.
-Appliquer dans le référentiel terrestre supposé galiléen la seconde loi de Newton au système et projeter la relation obtenue sur un axe vertical orienté vers le haut.
- En déduire en fonction de a, g, m1, l'expression de la masse m du lest jeté par dessus bord.
B- Du lest est lâché sans vitesse initiale à un instant t=0, lorsque la mongolfière est immobile à l'altitude h=320 m.
- Etablir l'équation horaire z(t) du mouvement de chute du centre d'inertie G du lest. L'axe zz' est orienté vers le haut et son origine est au niveau du sol.
- Exprimer puis calculer l'instant t de l'impact au sol.
C- De retour - menu au sol l'aérostier passe un examen médical nécessitant l'ingestion d'une dose d'iode 131 de masse m0=0,8 m g. La demi-vie de cet isotope radioactif émettant des rayons b - est t½=8 jours.
| Z |
51 |
52 |
53 |
54 |
| élément |
Sb |
Te |
I |
Xe |
donnée : ln10/ln2 = 3,3
- Ecrire l'équation de désintégration de l'iode 131
- Déterminer la masse de cette substance radioactive encore présente dans l'organisme 32 jours après l'ingestion. Au bout de combien de jours après l'ingestion, la masse m de cette substance restante est inférieure à 1% de la masse m0 initialement ingérée ?
corrigé
poussée : verticale, vers le haut, valeur = poids du volume d'air déplacé = rair Vg
poids: vertical, vers le bas, valeur =mg
Ecrire la 2ème loi de Newton sur un axe vertical vers le bas ( descente) : m1g - rair Vg = m1a. (1)
a= g(1 - rair Vg/m1)
Ecrire la 2ème loi de Newton sur un axe vertical vers le haut ( montée) : -m2g + rair Vg = m2a. (2)
a = g( rair Vg/m2-1)
masse du lest jeté : m= m1-m2 (3) ; (2) donne : m2 = rair Vg /(a+g)
repport dans (3) : m= m1- rair Vg /(a+g)
(1) donne : rair Vg = m1(g-a)
(3) s'écrit : m= m1-m1(g-a) /(g+a) = 2am1/(a+g).
mouvement de chute libre verticale, sans vitesse initiale.
axe zz' orienté vers le haut, sens contraire du vecteur accélération
vitesse primitive de l'accélération v = -gt
position, primitive de la vitesse z = -½gt² +h.
au sol z=0 d'où t² = 2h/g = 2*320/10 = 64 ; t= 8s.
13153I-->AZX+0-1e
conservation du nombre de nucléons : 131=A+0
conservation de la charge : 53 = Z-1 d'où Z=54 et en conséquence X est le xénon Xe
32 jours correspond à 4 périodes : la masse initiale est divisée par 16 = 24.
0,8 10-6/ 16 = 80 10-8 /16 = 5 10-8 g.
masse finale m <= masse initiale m0 /100
m=m0 e-lt soit ln (m0 /m)=lt avec l=ln2/T ( T demi-vie ou période en jours)
ln ( m0 /m)= t/T ln2 ; ln 100 = t/T ln 2 ; 2 ln 10 = t/T ln2
t/T = 2ln10/ln2 = 6,6 soit t = 6,6 T =6,6*8 = 52,8jours
au delà de 52,8 jours la masse initiale est divisée par 100.
O |
| dipôle LC
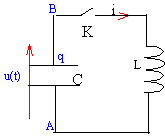
La résistance de la bobine est négligeable. La tension aux bornes du condensateur vaut U0=10 V, l'interrupteur K étant ouvert. A l'instant t=0 on ferme l'interrupteur K.
- Nommer le phénomène obtenu.
- Des enregistrements ont permis d'obtenir l'expression de u(t) et i(t) : u(t)=10 cos(2 104t) en volt ; i(t) = 20 sin ()2 104t en mA.
- Ecrire la relation entre u, C et du/dt. Justifier.
- Montrer que C= 100 nF.
- Calculer la valeur de L.
- Calculer la valeur de l'énergie E du circuit.
- Comment varie E au cours du temps ?
- Calculer la période propre T0.
- On appelle t1 la date à laquelle, pour la première fois après la fermeture de K, l'énergie est répartie de façon égale entre la bobine et le condensateur. Calculer u(t1) et i(t1).
Données : rac carrée (2) =1,4 ; rac carrée (50) = 7,1.
corrigé
oscillations libres non amorties : régime sinusoïdale
q= Cu(t) ; i = - dq/dt = -Cdu/dt ( signe - car décharge ) ; di/dt = -Cd²u/dt² = -Cu"
Ldi/dt = u(t) soit L(-Cd²u/dt² )= u ou bien LCu"+u=0.
u=10 cos(2 104t)
du/dt = u' = 10*2 104 (-1) sin(2 104t)
or i = - dq/dt = -Cdu/dt = -C(-1) 2 105sin(2 104t) = 2C 105sin(2 104t)
or i= 20 10-3sin(2 104t) ampères d'où 20 10-3 = 2C 105 soit C= 10-7F = 100 nF.
w0=2 104 rad/s ; w02 = 1/(LC) soit LC = 1/(4 108)
L= 1/(4 108* 10-7) = 1/40 H= 1000/40 mH=25 mH.
à t=0 , condensateur chargé, i=0 le condensateur stocke l'énergie du dipôle LC
E=½CU0²= 0,5 10-7 10² = 50 10-7 = 5 10-6 = 5mJ.
si la résistance du circuit est nulle, il n'y a a pas d'amortissement et l'énergie reste constante.
période T0=2p/w0=6,28 / 2 104 = 3,14 10-4 s = 0,314 ms.
le condensateur stocke la moitié de l'énergie du dipôle LC soit 2,5 10-6 J
2,5 10-6 =½Cu²(t1) = ½10-7 10² cos²(2 104t1)
2,5 10-6 =5 10-6 cos²(2 104t1)
0,5 = cos²(2 104t1)soit rac carrée (0,5) =0,707 = cos(2 104t1)
0,707 = cos (0,785) , angle en radian.
0,785=2 104 t1 ; t1= 3,925 10-5 s = 0,0392 ms . soit 1/8 période.
u(t1)=u=10 cos(2 104t1) = 10 cos (2 104*3,925 10-5) = 7,07 V.
i(t1)=20 10-3sin(2 104t1) = 20 10-3 sin (2 104*3,925 10-5) = 14,2 10-3 A.
|
lunette astronomique
Une lunette astronomique utilisée pour observer la lune est constituée d'un objectif de distance focale f'1 = 100 cm et d'un oculaire de distance focale f'2 = 2 cm, assimilable à des lentilles minces convergentes. La lunette est afocale, les centres optiques des deux lentilles sont distants de 102 cm.
- La lune étant considérée à l'infini a un diamètre apparent a=9,3 10-3 rad. L'objectif en donne une première image AB, A étant sur l'axe du montage
- Où est située cette image. Justifier.
- Quelle est sa grandeur ?
- Où est située l'image finale ? Justifier sans figure.
- Quel est l'interêt du montage afocal ?
- L'utilisateur veut projeter sur une plaque photographique une image A'B' de la lune 4 fois plus grande que l'image AB précédente. Dans quel sens dioit-il déplacer l'oculaire ? Justifier
- Calculer le déplacement de l'oculaire.
- Où doit-il placer la plaque photographique ?
Donnée : tan a = a (rad)
corrigé
Objet ( la lune) à l'infini, donc l'image donnée par l'objectif se trouve dans le plan focal image de cette lentille.
La grandeur de l'image est proche de : AB = f1 a = 1*9,3 10-3 = 9,3 10-3 m
La lunette étant afocale, l'image définitive A1B1 se trouve à l'infini et en conséquence l'image intermédiaire se trouve dans le plan focal objet de l'oculaire. L'oeil n'accomode pas et observe l'image sans fatigue.
On doit obtenir une image réelle A2B2 sur la plaque photographique ; l'objet AB (image intermédiaire) ne doit pas se trouver entre le centre optique de l'oculaire O2 et le foyer principal objet de l'oculaire ( sinon l'image sera virtuelle) : il faut donc déplacer l'objectif vers la droite, dans le sens de la lumière.
( ce qui est écrit en gras et en bleu est une grandeur algèbrique)
|grandissement| = |O2A2 /O2A | = 4 soit O2A2 = 4 |O2A |
O2A2 positif et O2A négatif donc O2A2 = -4O2A
formule de conjugaison :1/f2 = 1/O2A2 -1/O2A.
1/f2 = 1/(-4O2A) -1/O2A= -1,25 /O2A
O2A = -1,25 2= -1,25*0,02 = 2,5 10-2 m
soit un déplacement de 5 mm vers la droite.
La plaque photo se trouve à droite de l'oculaire ( dans le sens de la lumière gauche vers la droite)
O2A2 = 4 |O2A | = 4*2,5 10-2 = 0,1 m.
|
| ammoniac
Le pH d'une solution aqueuse S0 d'ammoniacNH3 de concentration apportée c0=0,01 mol/L vaut 10,6 à 25°C.
- Ecrire l'équation de la réaction de l'ammoniac avec l'eau.
- Exprimer puis calculer le quptient de réaction à l'état d'équilibre Qr,éq et le taux d'avancement final t0.
- A partir du système à l'équilibre on envisage différentes situations :
- On ajoute une pointe de spatule de chlorure d'ammonium solide.
- On ajoute une goutte d'une solution diluée d'acide chlorhydrique ( sans variation de volume)
- On chauffe la solution ( la solubilité du gaz évolue en sens inverse de la température)
Préciser le sens d'évolution du système dans les trois situations.
- On dilue 10 fois la solution S0 précédente et on mesure le pH de la solution diluée notée S1 : pH=10.Calculer le taux d'avancement final t1 de la réaction dans cette nouvelle solution.
- Comparer t0 à t1 et conclure.
Données : 10-0,4 = 0,4 ; 1/6 = 0,17.
corrigé
NH3 + H2O = NH4+ + HO- ; Qr,éq = [NH4+ ]éq[HO-]éq / [NH3]éq
avec [NH4+ ]éq=HO-]éq = 10-14 /10-pH = 10-3,4 = 10-3*10-0,4= 4 10-4 mol/L
[NH3]éq proche de C0, l'ammoniac étant peu dissociée.
Qr,éq =(4 10-4)² / C0 = 16 10-8 / 10-2 = 1,6 10-5.
taux d'avancement final t1= xéq / x max = 410-4 / 10-2 = 0,04.
ajout NH4+ : équilibre déplacé vers la gauche ; sens indirect ; consommation de l'ion ammonium ajouté.
ajout ion oxonium H3O+ : réaction acide base H3O+ + HO- --> 2H2O, l'ion HO- disparaît
équilibre déplacé vers la droite ; sens direct ; formation d'ion hydroxyde.
on chauffe la solution : l'ammoniac est moins soluble ( disparition de NH3 au profit de l'ion NH4+
équilibre déplacé vers la droite ; sens direct ; formation d'ion NH4+.
facteur de dilution : xmax = 10-3 mol
taux d'avancement final t0= xéq / x max = 10-4 / 10-3 = 0,1.
ajout d'eau : l'équilibre est déplacé vers la droite, consommation de l'eau ajoutée; sens direct.
|
L'eaux de chaux
- L'eau de chaux est une solution saturée d'hydroxyde de calcium Ca (OH)2 dont la solubilité à 25°C est s=0,01 mol/L.
- Ecrire l'équation de la mise en solution de l'hydroxyde de calcium.
- Donner l'expression de la constante d'équilibre K1 associée à cette équation.
- Exprimer K1 en fonction de s.
- Calculer K1.
- On fait barboter dans 1 L d'eau de chaux un courant de dioxyde de carbone.
- Deux réactions acido-basiques successives se produisent dans la solution. Ecrire leurs équations.
- La constante d'équilibre associée à la mise en solution du carbonate de calcium CaCO3 solide a pour valeur à 25°C K2 = 4 10-9. Ecrire l'équation de cette réaction et donner l'expression de K2.
- Quelle quantité minimale de dioxyde de carbone faut-il dissoudre dans la solution étudiée pour observer un début de précipitation de carbonate de calcium ?
- Justifier l'utilisation de l'eau de chaux pour détecter la présence de dioxyde de carbone.
corrigé
Ca (OH)2 = Ca2+ + 2HO- (1) K1=[Ca2+] [HO-]²
solution électriquement neutre : 2[Ca2+]=[HO-] = 2s
K1=s *(2s)² = 4 s3= 4 10-6.
HO- + CO2 = HCO3-.
2HO- + CO2 = CO32- + H2O (3) K3=[CO32- ] /([CO2][HO-]²)
CaCO3= Ca2+ + CO32- ; K2 = [Ca2+] [CO32- ]= 4 10-9.
le carbonate de calcium commence à précipiter dès que le produit [Ca2+] [CO32- ] atteint la valeur 4 10-9.
dans l'eau de chaux saturée : [Ca2+]= 0,01 mol/L cette valeur reste inchangée lors de l'ajout de CO2.
0,01[CO32- ]= 4 10-9.
[CO32- ] = 4 10-7 mol/L
2HO- + CO2 = CO32- + H2O (3) donne [CO32- ] = [CO2]= 4 10-7 mol/L
Une quantité très faible de CO2 dissout peut être détecte
Projectile, le trébuchet bac S 2007 La Réunion
Sans calculatrice ; 5,5 pts ; d'autres corrigés labolycee.org ; intellego.fr ; montblancsciences.free.fr.
Le trébuchet est une machine de guerre utilisée au Moyen Age au cours des sièges de châteaux forts. Le projectile pouvait faire des brèches dans les murailles des châteaux forts situés à plus de 200 m du trébuchet. Son principe de fonctionnement est le suivant :
Un contrepoids relié à un levier est maintenu à une certaine hauteur par des cordages. Il est brusquement libéré. Au cours de sa chute, il agit sur un levier au bout duquel se trouve une poche en cuir dans laquelle est placé le projectile.
Lors de sa libération, le projectile de la poche se trouve à une hauteur H = 10 m et est projeté avec une vitesse faisant un angle a avec l'horizontale
Les mouvements du contrepoids et du projectile s'effectuent dans un champ de pesanteur uniforme.
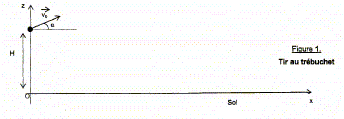

Données : Masse du projectile m = 130 kg ; g = 10 m/s² ; H = 10 m ;masse volumique de l'air rair = 1,3 kg.m -3 ; volume du projectile V = 50 L.
Étude du mouvement du projectile après libération
Le système étudié est le projectile. Les frottements de l'air sur le projectile seront négligés dans cette étude. Le champ de pesanteur est parallèle à l'axe Oz.
- Donner les caractéristiques (sens, direction et valeur) du poids et de la poussée d'Archimède qui s'exercent sur le projectile.
- Est-il judicieux de négliger par la suite la poussée d'Archimède ?
- En appliquant la 2ème loi de Newton dans le cadre de la chute libre, déterminer les coordonnées ax et az du vecteur accélération du centre d'inertie du projectile dans le repère indiqué.
- Donner l'expression des coordonnées du vecteur vitesse initiale v0 , notées v0x et v0z , en fonction de v0 et a.
- On appelle vx(t) la composante horizontale du vecteur vitesse et vz(t) sa composante verticale. Déterminer l'expression des composantes horizontale et verticale vx(t) et vz(t) du vecteur vitesse du système au cours de son mouvement.
- En déduire la nature du mouvement du projectile en projection sur l'axe horizontal. Justifier.
- Déterminer l'expression des équations horaires du mouvement du projectile : x(t) et z(t).
- Montrer que l'équation de la trajectoire du projectile est la suivante :z= -½ g x2/ ( v0 cos a)2 + x tan a + H.
- Quelle est la nature de la trajectoire du projectile ? Représenter qualitativement l'allure de la trajectoire.
- En utilisant l'expression de l'équation de la trajectoire, indiquer les paramètres de lancement qui jouent un rôle dans le mouvement du projectile.
- Dans le cas où le projectile est lancé avec une vitesse initiale horizontale, montrer que l'abscisse de son point de chute est : x = v0 ( 2H/g)½.
- Avec quelle vitesse initiale v0 horizontale, le projectile doit-il être lancé pour atteindre la base du mur du château situé à une distance x = 100 m ?
Aide au calcul : 0,5½ = 0,71 ; 2½ = 1,41.
Le poids :
Appliqué au centre d'inertie du boulet, vertical, dirigé vers le bas, valeur P=mg = 130*10 = 1,3 103 N.
La poussée d'Archimède :
Appliquée au centre d'inertie du boulet, verticale, dirigée vers le haut;
Sa valeur est égale au poids du volume d'air déplacé : PA= V rair g
avec V= 50 L = 0,050 m3 ; rair = 1,3 kg.m -3 ; g = 10 m/s².
PA = 0,050*1,3*10 = 0,65 N.
La valeur de la poussée d'Archimède étant environ 2000 fois plus petite que la valeur du poids, la poussée peut être négligée devant le poids.
Coordonnées ax et az du vecteur accélération du centre d'inertie du projectile :
Appliquer la 2ème loi de Newton dans le cadre de la chute libre.
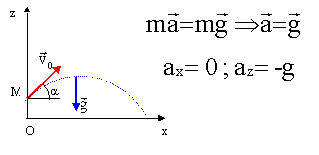
Coordonnées du vecteur vitesse initiale v0 :
v0x = v0 cos a ; v0z =v0 sin a.
On appelle vx(t) la composante horizontale du vecteur vitesse et vz(t) sa composante verticale.
Composantes horizontale et verticale vx(t) et vz(t) du vecteur vitesse du système au cours de son mouvement :
Le vecteur vitesse est une primitive du vecteur accélération :
vx(t) = v0 cos a ; vz(t) = -gt + v0 sin a.
Nature du mouvement du projectile en projection sur l'axe horizontal :
La valeur de la composante horizontale de la vitesse est constante : le mouvement est donc uniforme suivant Ox.
Equations horaires du mouvement du projectile : x(t) et z(t).
Le vecteur position est une primitive du vecteur vitesse :
x(t) = v0 cos a t (1)
z(t) = -½gt2 + v0 sin a t + H. (2)
Equation de la trajectoire du projectile est la suivante :
(1) donne t = x / v0 cos a. Repport dans (2).
z = -½ g x2/ ( v0 cos a)2 + x tan a + H.
Nature de la trajectoire du projectile : arc de parabole.
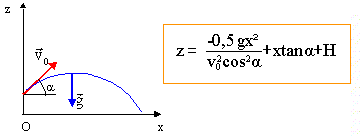
Les paramètres de lancement qui jouent un rôle dans le mouvement du projectile sont la vitesse initiale v0, l'angle a et l'altitude initiale H.
Dans le cas où le projectile est lancé avec une vitesse initiale horizontale, l'abscisse de son point de chute est
Dans l'expression de z, écrire que a =0 , c'est à dire cos a =1 et tan a = 0 :
z = -½ g x2/ v02 + H.
L'altitude du point de chute étant nulle : -½ g x2/ v02 + H = 0
x2 =v02 2H / g ; x= v0 ( 2H/g)½.
Pour atteindre la base du mur du château situé à une distance x = 100 m, le projectile doit être lancé avec une vitesse initiale horizontale v0 de :
v02 = x2 g /(2H) ; v0 = x (g/(2H))½.
v0 = 100 (10/20)½ = 100*0,5½ = 100*0,71 = 71 m/s.
|
|
Une auto ayant une masse de 900 kg se déplace sur une route horizontale. On évalue les forces de frottement indépendantes de la vitesse à 300 N / tonne.
- En partant du repos, la voiture atteint une vitesse de 90 km/h en 50 secondes. Trouvez la force de traction du moteur, supposée constante et le chemin parcouru pendant le démarrage.
- Quelle force le moteur doit-il développer pour maintenir cette vitesse de 90 km/h ?
- A un certain moment, le conducteur arrête le moteur sans serrer les freins. Au bout de combien de temps la voiture s'arrêtera-t-elle et quelle sera le chemin parcouru ?
- Lorsqu'on agit sur les freins, la voiture s'arrête après avoir parcouru 125 m, la vitesse initiale étant toujours de 90 km/h. En supposant la force de freinage constante, quelle est sa valeur ?
corrigé
|
| frottement 300*0,9 = 270 N.
mettre la vitesse en m/s : 90 /3,6 = 25 m/s.
accélération (m/s²) = variation de la vitesse (m/s) / durée de cette variation (s) = 25 / 50 = 0,5 m/s².
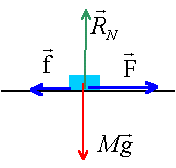
la seconde loi de Newton s'écrit sur un axe parallèle à la route ( sens du mouvement) :
-f +F = ma
F = ma + f = 900*0,5 +270 = 720 N.
distance parcourue : d = ½ a t² = 0,5 * 0,5 *50 ² = 625 m.
soit -f + F= 0 d'où F = 270 N. moteur à l'arrêt et freins non serrés :
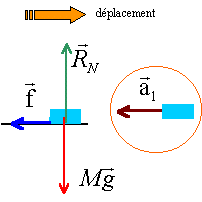
la seconde loi de Newton s'écrit sur un axe parallèle à la route ( sens du mouvement) :
- f = ma1
a1 = -270 / 900 = -0,3 m/s².
utiliser la relation : v² finale - v² départ = 2 accélération fois distance
0 - v² = 2a1 d
d = 25*25 / (0,6 ) = 1041 m.
expression de la vitesse : v final = a1 tfinal + v départ.
0 = -0,3 tfinal +25
tfinal = 83,3 s.
moteur à l'arrêt et freins serrés :
à la force de frottement précédente on ajoute la force de freinage
v² finale - v² départ = 2 accélération fois distance
0 - 25² = 2a2 *125
a = -2,5 m/s².
écrire la 2 ème loi de Newton sur un axe parallèle à la route (sens du mouvement) :
-(freinage +frottement) = ma2.
ma2 = 900*(-2,5) = -2250 N
force de freinage = 2250-270= 1980 N.
mouvement rectiligne uniforme donc la somme des forces est nulle (principe d'inertie) |
devoirs en terminale S
- Aristote (-300 avant JC) affirmait qu'"une masse d'or, de plomb ou de tout autre corps pesant, tombe d'autant plus vite qu'elle est grosse"...
- Galilée ( XVII ème siècle) mène une série d'expériences du haut de la tour de Pise, en Italie. Le savant se munit d'objets divers et variés : une plume, une pomme, une boule de fer de 100 livres et une boule de fer de 1 livre...
L'expérience consiste à envoyer par-dessus bord les objets et observer leur ordre d'arrivée. À l'issue de ce petit jeu, Galilée affirme que les deux boules arrivent ensemble.
Un an après la mort de Galilée, son élève Evangelista Toricelli étudie la chute dans le vide d'une plume et d'une pomme. Dans une enceinte où l'air a été pompé, plume et pomme chutent à la même vitesse exactement.
- Deux boules de fer de masse respective m = 100 livres et m' = 1 livre sont lâchées sans vitesse initiale du haut de la tour de Pise. On considère les actions de l'air comme négligeables par rapport aux autres forces.
On considère que le mot "vite" utilisé par Aristote fait référence à la durée de la chute d'un corps à partir d'une hauteur donnée. Parmi les propositions suivantes, laquelle est soutenue par Aristote ? Par Galilée ? Justifier votre réponse.
a. t = k / m b. t = k'* m c. t = k''.
k, k' et k'' sont des constantes ; t désigne la durée de la chute ; m désigne la masse du corps.
- En appliquant les lois de la mécanique aux deux boules de fer citées ci-dessus et évoluant dans le champ de pesanteur terrestre considéré comme uniforme de valeur g, exprimer la vitesse de leur centre d'inertie lorsqu'elles arrivent au sol, ainsi que la durée de leur chute. Ne pas oublier de faire un schéma.
- Conclure en précisant qui, d'Aristote ou de Galilée, a raison.
corrigé
|
|
|
Aristote : durée de la chute et masse sont inversement proportionnelles donc proposition (a).
Galilée : la durée de la chute est indépendante de la masse donc proposition (c)
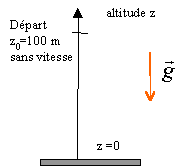
chute libre sans vitesse initiale
altitude : z = -4,9 t²+ 100
en arrivant au sol z=0 d'où la durée de la chute :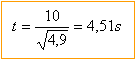
vitesse : dériver z par rapport au temps
v =-9,8 t soit au sol en norme 44,2 m/s.
(le signe moins indique que le vecteur vitesse est dirigé vers le bas en sens contraire de l'axe z)
La durée et la vitesse sont indépendantes de la masse dans un mouvement de chute libre ( Galilée a raison)
|
| 2
Newton et la gravitation
|
Les travaux de Galilée sur la chute des corps, menés du haut de la Tour de Pise, inspirent, plus de 50 ans après, un Britannique, Isaac Newton. En 1686, celui-ci annonce une série de lois sur le mouvement des corps, dont l'une est la "loi de la gravitation universelle".
- Donner les expressions vectorielles des forces gravitationnelles s'exerçant entre deux objets ponctuels A et B de masse respective mA et mB, et situés à une distance d l'un de l'autre.
- En déduire l'expression du champ de gravitation terrestre régnant à une altitude z. On notera Gz la valeur de ce champ de gravitation.
- Si on ne garde que deux chiffres significatifs sur la valeur de g,valeur du champ de pesanteur, on peut la confondre avec la valeur Gz du champ de gravitation .
On étudie les variations du champ de gravitation en fonction de l'altitude : A partir de quelle altitude Gz varie-t-il de 1 % par rapport à sa valeur au niveau du sol ? En déduire si les variations de Gz avec l'altitude sont significatives pour l'expérience de Galilée décrite dans le texte.
- On cherche maintenant à savoir si des objets posés au sol peuvent modifier de manière significative, du fait de leur masse, la valeur du champ de gravitation au voisinage de la Terre. Au sol est maintenant posé un boulet sphérique de rayon 5 cm et de masse m' = 4 kg.
Calculer la valeur maximale du champ gravitationnel que peut créer le boulet seul, en un point situé à la verticale du boulet. Conclure.
Données : G = 6,67 10-11 N.m2.kg-2. Rayon de la terre R = 6 ,371 106 m.
- M (Terre) = 5,99 1021 tonnes. 1 livre = 478 g.
corrigé
|
|
|
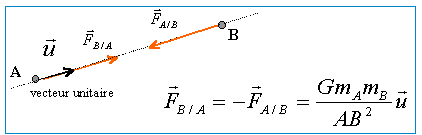
champ de gravitation au sol et à l'altitude z
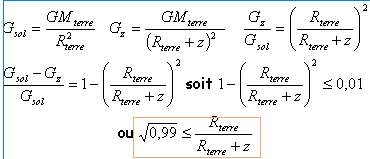
0,9945 (Rterre + z) < 6 ,371 106
Rterre + z <6 ,403 106 soit une altitude z inférieure à 32 km
(la tour de Pise mesure seulement 100 m)
Champ crée par un boulet de 4 kg à une distance d supérieure à 5 cm .
6,67 10-11 *4/ d² = 2,67 10-10 / d²
valeur très inférieure à 9,8 ms-2.
A la place du boulet, il faudrait prendre une montagne pour observser une variation de quelques millièmes.
|
 3 3
champ électrique
|
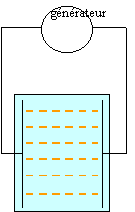
Le but de cet exercice est d'établir les caractéristiques du champ électrique E régnant entre les deux plaques A et B d'un condensateur plan et de déterminer la valeur de la différence de potentiel entre deux points à l'intérieur de ce condensateur. Les deux plaques du condensateur sont reliées aux bornes d'un générateur de tension délivrant une tension continue.
A et B sont deux plaques métalliques verticales. Les bases de A et de B baignent dans de l'huile de ricin. On saupoudre des graines de gazon entre A et B. Les graines se répartissent à la surface de l'huile en matérialisant des lignes. Le champ électrique est en tout point tangent à ces lignes, qui ont l'allure ci contre.
- Quelle(s) caractéristique(s) du vecteur champ électrique est (sont) mise(s) en évidence dans cette expérience ?
- Les plaques A et B sont toujours verticales, reliées à une alimentation stabilisée, et on place une petite bille ponctuelle, de masse m, chargée positivement, suspendue à un fil, entre les armatures. On constate que la bille est attirée par la plaque B. Peut-on conclure sur la direction du champ électrique ? Sur son sens ? Si oui, donnez sa direction et / ou son sens.
corrigé |
|
|
Les lignes de champ sont parallèles entre elles et perpendiculaires aux plaques, le champ électrique entre les plaques est uniforme (vecteur constant en norme et sens).
La bille chargée positivement, placée dans un champ électrique est soumise à la force électrique 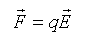
Ces 2 vecteurs colinéaires ont le même sens car q est positive. Donc le champ électrique est dirigée vers la plaque B.
|
 4 4
relation entre champ et potentiel
|
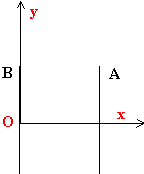
- Les deux plaques A et B sont verticales, distantes de 12 cm et immergées dans une cuve horizontale remplie d'une solution aqueuse de sulfate de cuivre II. Le générateur délivre une tension de 6 V. Un multimètre muni de pointes-stylet permet de mesurer la différence de potentiel USB entre différents points S de l'espace entre A et B et la plaque B. On choisit par convention VB = 0V. Donnez l'expression de la valeur E du champ électrique au point S.
- Soit le repère (Oxy) lié au condensateur, défini ci contre. Afin de repérer la position du stylet S entre les plaques A et B, on place sous la cuve un papier millimétré. Les coordonnées du stylet S sont xS et yS dans le repère (Oxy). On déplace le stylet de B vers A. Comment la tension USB évolue-t-elle ?
- Pour différentes positions du stylet, on obtient les valeurs en volts suivantes :
|
yS (cm)
........xS (cm)
|
4 |
2 |
0 |
-2 |
-4 |
| 2 |
1,2 |
1 |
0,8 |
1 |
1,2 |
| 4 |
2,1 |
2 |
2 |
2 |
2,1 |
| 6 |
3 |
2,9 |
3 |
2,9 |
3 |
| 8 |
3,9 |
3,9 |
4 |
3,9 |
3,9 |
| 10 |
4,9 |
4,9 |
4,9 |
4,9 |
4,9 |
- Quelles sont les observations que l'on peut faire à la première lecture de ce tableau ?
- On étudie maintenant la variation du potentiel le long de la droite y = 0 cm.
Tracer le graphe de la fonction USB = f(xS). En déduire une relation entre USB et xS. Faire l'application numérique.
- En utilisant ce graphique pour xS compris entre [0 cm ; 12 cm], déterminer la valeur de USB pour x = 12,0 cm et établir pour une position quelconque de S la relation liant USB , xS et E.
- On place le stylet au point S de coordonnées ( xS = 4,0 cm ; yS = 0,0 cm ) dans le repère ci-dessus. La plaque B reste fixe. On déplace la plaque A jusqu'à ce que xA = 24,0 cm. Quelle sera la valeur de la tension UAB entre les plaques ? Quelle sera la valeur E du champ électrique entre les plaques ? Quelle sera la tension USB mesurée ?
corrigé
|
|
|
E(Vm-1) = UAB (V) / AB (mètre)
E = 6/0,12 = 50 V m-1.
USB= 50*SB
Si le point S vient en B , USB=0 V
Si le point S vient en A, USB= 50*0,12 = 6 V
La tension USB croît linéairement en allant de B vers A.
Pour une valeur de x fixée, USB est quasiment la même, quelle que soit y, si on excepte la ligne où x vaut 2cm.
Pour une valeur de y donnée et pour x croissant la tension USB augmente.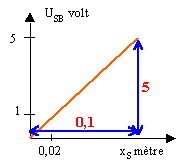
coefficient directeur de la droite 50 V m-1 soit la valeur du champ E
USB = E xS. soit 6 V pour xS=0,12 m
d' = 2 d
UAB est imposé par le générateur, donc non modifié;
E' = UAB / d' = UAB / (2d )= E / 2
USB = E' x or E' est divisé par 2 , donc USB est divisée par 2.
|
|
oxydation du zinc par l'acide chlorhydrique
Potentiel redox des couples H3O+/H2 0 volt Zn2+/Zn -0,76 volt
- Ecrire l'équation bilan en précisant quels sont le réducteur et l'oxydant
- La concentration molaire [Zn2+] dans la solution est déterminée à divers instants,soit:
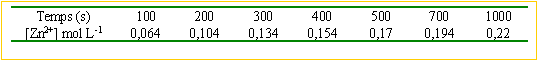
Déterminer la vitesse moyenne de formation de l'ion Zn2+ dans l'intervalle de temps [0;500s]
- Tracer la courbe d'équation [Zn2+] = f(t)
- Déterminer la vitesse instantanée de formation de l'ion zinc à t=0 s et à t=300s. Quel facteur cinétique est mis en évidence.
- Quelle serait la vitesse instantanée de disparition de l'ion hydronium aux mêmes instants ?
corrigé
|
|
|
Zn + 2 H3O+ donnent Zn2+ + H2 + 2H2O
réducteur : le zinc métal ; oxydant : ion hydronium
vitesse moyenne (mol L-1 s-1)
= variation concentration en valeur absolue (mol L-1 )
divisée par intervalle de temps (s)
(0,17-0) / 500= 3,4 10-4 mol L-1 s-1
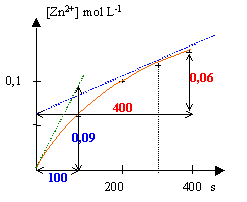
à t=0 : 0,09/100 = 9 10-4 mol L-1 s-1
à t=300 s : 0,09/100 = 1,5 10-4 mol L-1 s-1
La vitesse d'une réaction diminue lorsque la concentration d'un réactif diminue.
D'apès les coefficients de l'équation bilan, 2 moles d'ion hydronium disparaissent lorsque'une mole d'ion zinc se forme. La vitesse de disparition des ions hydronium est le double de la vitesse d'apparition des ions zinc.
|
| 2
cinétique questions de cours
|
- Qu'étudie la cinétique chimique ?
- En quelle unité s'exprime la vitesse de formation ou de disparition d'un corps ?
- A quoi sert une "trempe " en cinétique chimique.
- Citer 2 facteurs cinétiques ;quel est leur influence sur la vitesse de formation d'un corps
corrigé
|
| 3
sonde solaire
|
La terre et le soleil sont des corps à symétrie sphérique.On utilise un référentiel galiléen ayant pour origine le centre du soleil et on néglige l'influence des planètes autres que la terre.
- Le poids d'un objet de masse m à la surface de la terre de masse M et de rayon R n'est pratiquement du qu'à l'attraction newtonienne de la terre.Si g désigne l'intensité du champ de pesanteur à la surface de la terre ,exprimer le produit GM en fonction de g et R ( G constante d'attraction universelle).
- La terre considérée comme ponctuelle décrit autour du soleil ,de masse kM ( k=constante =106/3) une orbite pratiquement circulaire de rayon r .Exprimer ,en fonction de r et k ,la distance x par rapport au centre de la terre , du point d'équigravité du système terre soleil ( point où les intensité des champs de gravitation du soleil et de la terre sont égales).
Calculer x si R=6400 km ; g=9,8 ms-2 ; r=1,5 108 km
corrigé
|
|
|
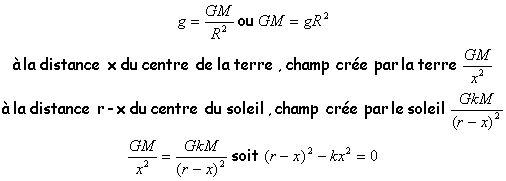
différence de 2 carrés
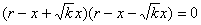
avec x< r , le point cherché étant entre la terre et le soleil.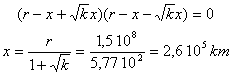
|
| 4
pendule électrique
|
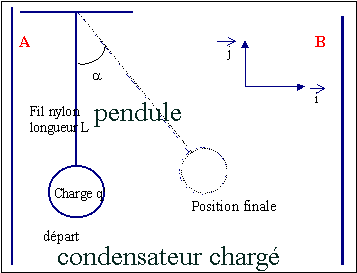
- Faire le bilan des forces appliquées à la boule du pendule et les représenter sur un schéma soigné.
- Exprimer la force électrique s'exerçant sur la boule du pendule en fonction de m ,g et a. La calculer .
- Quelle est la valeur de la tension UAB entre les plaques.
- La tension appliquée aux plaques par le générateur double ;quelle est la valeur de a.
- Les 2 plaques sont isolées du générateur;UAB a sa valeur initiale; on écarte les 2 plaques d=15 cm .Quelle est la valeur de a. ?
masse de la boule m=1,2g ;g=9,8 ms-2 a. =6,5°; q=-75 nC
distance des plaques d=10 cm; aire d'une plaque S=250 cm2
corrigé
|
|
|
A l'équilibre la somme vectorielle des forces appliquées à la bille chargée est nulle.
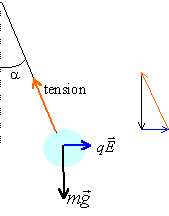
tan a = |q|E / (mg) d'où |q|E = tan a * (mg)
tan 6,5 * (1,2 10-3 *9,8) = 1,33 10-3 N
La charge est négative : vecteurs force électrique et champ sont colinéaires mais de sens contraire. Le champ E pointe vers la gauche, vers les plus petits potentiels.
donc UAB négative.
|q|E = |q| UBA/ AB d'où UBA= 1,33 10-3 * 0,1 / 75 10-9 = 1773 V
UAB = -1773 V
Si la tension UAB double, la force électrique double.
tan a = 2*1,33 10-3 / (1,2 10-3 *9,8) = 0,226
a = 12,7 °
La charge électrique reste constante le condensateur étant isolé du générateur
La capacité du condensateur et la distance des armatures AB sont inversement proportionnelles.
C1*0,1 = C2*0,15
C1 / C2= 1,5
Or Q = C2 U'AB= C1 UAB
U'AB= C1 / C2 UAB = 1,5*1773 = 2660V
E= 2660 /0,15= 17 733 Vm-1.
|q|E = 75 10-9 *17 733 = 1,33 10-3 N
tan a =1,33 10-3/ (1,2 10-3 *9,8) = 0,113
a = 6,5 ° valeur initiale inchangée
|
|
étude du coefficient de résistance à l'avancement r
|
Dans tout l'exercice, les wagons seront assimilés à des solides en translation, leurs mouvements seront étudiés dans le référentiel terrestre supposé galiléen. Les résistances aux passages dans les courbes et les perturbations liées aux changements de pente seront négligées.
Dans une gare de triage, les wagons sont séparés au sommet d'une butte ( Ils descendent un à un la rampe R et ils sont ensuite aiguillés vers une voie de garage où ils devront arriver au contact d'autres wagons pour former un nouveau train. Cette opération, appelée le "tir au but" par les professionnels, utilise des freins de voie F1 et F2.
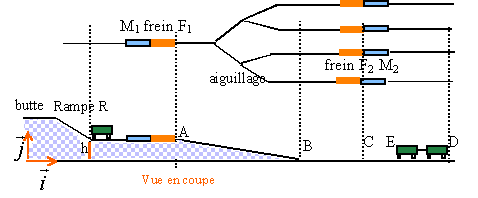
On appelle base de mesure M un dispositif comportant différents types de capteurs. La base de mesure M1 est utilisée pour la détermination du coefficient de résistance r à l'avancement et la base de mesure M2 est un autre dispositif utilisé pour la détermination de la longueur de rail restant à parcourir. L'ensemble de ces dispositifs permet la régulation de la vitesse de chaque wagon.
Les frottements qui s'exercent sur un wagon sont modélisés par une force et de valeur f = m.r, opposée au déplacement , où m est la masse du wagon et r le coefficient de résistance à l'avancement.
- Une étude préalable des variations du coefficient de résistance à l'avancement r en fonction de la valeur v de la vitesse donne les résultats rassemblés dans le graphe ci dessous, pour quatre wagons différents. Pour les wagons testés, le coefficient de résistance à l'avancement r dépend-il sensiblement de la vitesse dans le domaine étudié ? Justifier d'après le document.
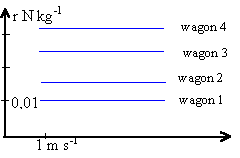
- Quelle valeur peut-on prendre pour le coefficient de résistance à l'avancement du wagon n° 4 ?
- La base de mesure M1 est située sur une partie horizontale des voies. Faire le bilan des forces qui agissent sur un wagon qui passe dans la base de mesure M1. Les représenter en faisant un schéma sur la copie.
- Montrer que, dans la base de mesure, M1, l'accélération d'un wagon a pour valeur a = r.
- La base de mesure M1 permet de connaître la valeur v de la vitesse à différentes dates t. L'ensemble des points de mesure (v,t), obtenus pour un wagon qui passe dans cette base, se répartissent sur une droite moyenne de type v = - k.t + p. Montrer que son coefficient directeur permet de déterminer la valeur du coefficient de résistance à l'avancement du wagon.
corrigé
|
|
|
Le coefficient de résistance à l'avancement ne dépend pas de la vitesse, les droites étant horizontales.
r = f(v) est une fonction constante.
r voisin de 0,033 N kg-1 (wagon 4).
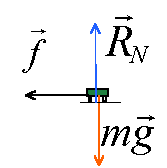
la somme vectorielle des forces appliquées au wagon est égale au produit de la masse par l'accélération.
Suivant l'axe j : RN = mg et suivant i : -f = ma avec f= m r
d'où la norme de l'accélération est égale à r.
le vecteur accélération est la dérivée du vecteur vitesse par rapport au temps :
v=-k t +p donne v' = a = -k avec en plus norme de l'accélération = r.
|
| 2
rôle du frein primaire
|
Situé derrière la base de mesure M1, ce frein doit laisser à chaque wagon une vitesse de valeur vA suffisante, à sa sortie en A, pour qu'il puisse atteindre l'extrémité D des voies de garage avec une vitesse de valeur vD. On ne tiendra pas compte dans cette partie du frein secondaire.
- Exprimer le travail de chacune des forces appliquées à un wagon pour le trajet AD. On note h la dénivellation entre les points A et B. On pose L = AB + BD. On pourra décomposer le calcul selon les deux parties AB et BD qui seront assimilées à des portions de droite.
- Démontrer l'expression suivante : V²A = 2(r.L - g.h) + V²D
- Calculer la valeur vA de la vitesse à la sortie du frein primaire d'un wagon de coefficient de résistance à l'avancement r égal à 0,032 N.kg-1 pour qu'il s'arrête en D lorsque L = 800 m et h = 1,0 m. On prendra pour l'intensité de la pesanteur g = 9,8 m.s-2.
corrigé
|
|
|
sur le trajet AB:
travail des frottements : - f AB = -mrAB
travail du poids : mgh
l'action RN normale au plan ne travaille pas.
sur le trajet BD:
travail des frottements : - f BD = -mrBD
le poids, perpendiculaire au plan, ne travaille pas
l'action RN normale au plan ne travaille pas.
au total : mgh - mr(AB+BD)= m(gh-rL)
La somme des travaux ci dessus est égale à la variation de l'énergie cinétique :
0,5 mv²D-0,5 mv²A =m(gh-rL)
v²D-v²A = 2(gh-rL)
v²A = 2(rL-gh) +v²D.
calcul de la vitesse en A, la vitesse en D étant nulle :
v²A = 2(0,032*800-9,8*1) = 31,6 et vA=5,62 ms-1.
|
| 3
rôle du frein secondaire
|
En réalité, on souhaite amener le wagon au contact des wagons déjà présents sur la voie de garage et obtenir son accrochage automatique. Du fait du remplissage des voies de garage, la distance qui reste à parcourir est variable suivant le nombre de wagons déjà présents. La position du dernier wagon sur la voie sera fournie par la base de mesure M2. Le frein secondaire va prendre en compte ces autres paramètres pour réaliser le tir au but avec précision.
- Pour assurer un accrochage automatique des wagons il faut une certaine valeur vE de la vitesse au moment du choc. En remarquant que les voies de garage CD sont horizontales,donner la relation entre la valeur vC de la vitesse à la sortie du frein secondaire et la valeur vE de la vitesse en E si la distance qui reste à parcourir est L' = CE.
- La valeur vE de la vitesse doit être comprise entre 0,50 m.s-1 et 1,5 m.s-1 pour assurer l'accrochage et rester dans les normes de sécurité pour la marchandise en évitant des chocs trop violents. En déduire un encadrement pour la valeur vC de la vitesse à la sortie du frein secondaire dans le cas où r est égal à 0,032 N.kg-1 et L' est égale à 400 m.
corrigé
|
|
|
seule la force de frottement travaille, poids et action RN étant perpendiculaires au plan.
-f CE = -mrL'
ce travail est égal à la variation de l'énergie cinétique 0,5 mvE² -0,5 mv²C.
vE² = v²C- 2rL' ou vC² = v²E+ 2rL'
valeur minimale de la vitesse en C :
vC² = 0,5² +2*0,032*400=25,85 et VC=5,08 ms-1.
valeur maximale de la vitesse en C :
vC² = 1,5² +2*0,032*400=27,85 et VC=5,28 ms-1.
|
|
frottement
solide sur plan incliné
énergie cinétique
|
On se propose de mesurer l'intensité des actions de frottement qui agissent sur un mobile autoporteur en mouvement. Ces actions seront modélisées par une force constante, de sens opposé au vecteur vitesse. Ce mobile, de centre d'inertie G, de masse m, est abandonné sans vitesse sur une table à digitaliser, inclinée d'un angle a par rapport à l'horizontale. Au cours de son mouvement, le mobile suit la ligne de plus grande pente, de direction Ox, la position de G est repérée en fonction du temps par sa coordonnée x dans le repère , et transmise à un ordinateur.
Données : m = 220 g, a = 15°, g = 9,8 m.s-2.
Les valeurs de x aux dates des relevés, figurent dans le tableau ci-joint, accompagnés du résultat du calcul de la plupart des vitesses instantanées et énergies cinétiques Ec du mobile en translation
| t (s) |
x (m) |
v (ms-1) |
Ec (J) |
l (m) |
| 0 |
0,0015 |
|
|
0 |
| 0,0139 |
0,0098 |
0,625 |
0,043 |
0,0083 |
| 0,0277 |
0,0188 |
0,669 |
0,049 |
0,0173 |
| 0,0414 |
0,0282 |
|
|
0,0267 |
| 0,0551 |
0,0378 |
0,722 |
0,057 |
0,0363 |
| 0,0687 |
0,0479 |
0,760 |
0,063 |
0,0464 |
| 0,0822 |
0,0584 |
0,788 |
0,068 |
0,0569 |
| 0,0956 |
0,0691 |
0,828 |
0,075 |
0,0676 |
| 0,1089 |
0,0808 |
0,860 |
0,081 |
0,079 |
| 0,1221 |
0,0919 |
0,882 |
0,086 |
0,0904 |
| 0,1352 |
0,1037 |
0,916 |
0,092 |
0,1022 |
| 0,1482 |
0,1158 |
0,950 |
0,099 |
0,1143 |
| 0,1612 |
0,1284 |
|
|
|
- Calculer les valeurs de v et Ec à la date t = 0,0414 s.
- Etablir l'inventaire des forces s'exerçant sur le mobile et les représenter sur un schéma.
- On appelle A et B les positions respectives occupées par le mobile aux dates t = 0 et t quelconque. En utilisant le théorème de l'énergie cinétique entre A et B, distants de l, exprimer Ec(B) en fonction de Ec(A), m, l, et l'intensité de frottement .
- Détermination de l'intensité de la force de frottement.
- A partir des valeurs portées dans le tableau, représenter Ec(B) en fonction de l. On prendra 1 cm pour 10-2 m et 1 cm pour 10-2 J.
- Déterminer l'équation de cette courbe.
- En déduire l'intensité de la force de frottement qui agit sur le mobile et l'énergie cinétique du mobile à la date t = 0.
corrigé
|
|
|
Dx = 0,0378-0,0188 = 0,019 m
Dt =0,0551-0,0277 = 0,0274 s
vitesse à la date t= 0,0414 s : 0,019 / 0,0274 = 0,693 m s-1.
énergie cinétique à cette date :
0,5 mv² = 0,5*0,22*0,693 ² = 0,0528 J
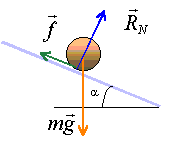
énergie cinétique initiale : Ec(A)
énergie cinétique à la date t : Ec(B)=0,5 mv²
varaition énergie cinétique : Ec(B)-Ec(A)
travail du poids au cours de la descente :mg l sina
travail des frottements : -f l
th de l'énergie cinétique : Ec(B)-Ec(A) =( mg sin a -f) l.(1)
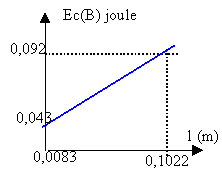
coefficient directeur de la droite : (0,092 -0,043) / (0,1022-0,0083) = 0,52
Ec(B) = 0,52 * l + Ec(A) (2)
par identification (1) et (2) donnent :
mg sin a -f =0,52
f = mg sin a -0,52 =0,22*9,8*sin15-0,52
f=0,558-0,52 = 0,038 N
|
|
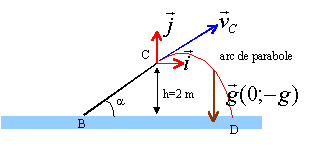
Un skieur de masse m = 80 kg est tiré par un bateau à l'aide d'une corde parallèle à la surface de l'eau. Il démarre sans vitesse initiale du point A. Le skieur lâche la corde en B et passe sur le tremplin BC. Il arrive en C avec une vitesse Vc = 72 km.h -1 , effectue un saut, retombe sur l'eau en D.
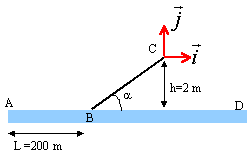
Dans tout le problème on étudiera le mouvement du centre d'inertie G du skieur. On supposera que :
- sur le trajet AB la force de traction F de la corde est constante et l'ensemble des forces de frottement est équivalent à une force unique f opposée au déplacement et d'intensité f = 100 N
- de B en D tous les frottements sont négligeables. g = 10 m./s² .
- Représenter les forces qui s'exercent sur le skieur en un point du trajet AB et en un point du trajet BC.
- Donner les expressions litterales exprimant les travaux de ces forces s'exerçant sur le skieur au cours des trajets AB et BC .
- En utilisant le théorème de l'énergie cinétique, , exprimer l'intensité F, tension du câble, en fonction de f , m , g , h , L, Vc ) pour que le skieur arrive en C avec la vitesse Vc.
-Calculer F
- Après le saut, donner les composantes du vecteur accélération quand le skieur a quitté le tremplin dans le repère ( C , i ,j ).
- Représenter sur la figure au point C, sans échelle précise, le vecteur vitesse du skieur lorsqu'il arrive au point C.
- Quelle est la nature de la trajectoire du skieur au cours du saut ? Dessiner son allure sur la figure.
-Indiquer, sans justifier, la bonne expression de la vitesse Vs du skieur au sommet S de la trajectoire parmi les expressions suivantes : Vs = Vc ; Vs = Vc cos a ; Vs = 0.
champs électrique ou/et magnétique :
A la date t = 0 s, une particule chargée négativement pénètre en O avec une vitesse vo dans une zone Z où règne :
- soit un champ électrique E uniforme dont la direction est parallèle à celle du vecteur j.
- soit un champ magnétique B uniforme dont la direction est orthogonale au plan ( O, i, j ).
Le poids de la particule sera négligé devant les autres forces que vous prendrez en compte.
- La trajectoire de la particule dans Z, est l'arc de parabole OS2. En argumentant votre réponse, représenter sur la figure la force qui agit sur elle entre O et en S2 ; précisez le sens du champ E .
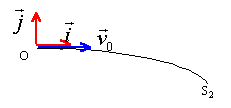
- L'énergie cinétique de la particule en S2 est-elle égale, plus grande, plus petite que celle qu'elle avait en O ? Justifier brièvement votre réponse.
- La trajectoire de la particule dans Z est l'arc de cercle OS3. En argumentant votre réponse ,représentez sur la figure la force qui agit sur elle en O et en S3 ; précisez le sens du champ B.
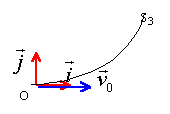
-L'énergie cinétique de la particule en S3 est elle égale, plus grande, plus petite que celle qu'elle avait en O ? Justifier brièvement votre réponse.
- En faisant agir les champs E et vect B simultanément, il est possible que la trajectoire de la particule dans Z rectiligne . Etablir la relation entre la vitesse Vo, les champs E et B pour satisfaire à cette condition. .
corrigé
|
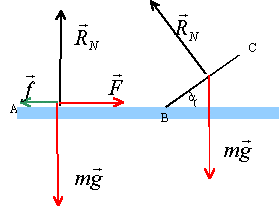
sur le parcours AB, le poids et l'action du support, perpendiculaires au support ne travaillent pas ; seuls F et f travaillent.
W A-->B = (F-f)L
DEc = ½ mv²B - 0 = (F-f) L
seul le poids travaille (RN est perpendiculaire au plan) sur le parcours BC :
WB-->C = -mgh
½ mv²C -½mv²B = - mgh
½ mv²C -(F-f) L= -mgh
(F-f) L = m(½ v²C +gh) d'où F = f + m(½ v²C +gh) / L.
vc = 72 /3,6 = 20 m/s.
F = 100 + 80 / 200 ( 0,5*20*20 + 10*2 ) = 188 N.
le vecteur vitesse en C est tangent au plan incliné (20 cosa ; 20 sin a )
la trajectoire est un arc de parabole
le mouvement est uns chute libre avec vitesse initiale
au sommet de la parabole le vecteur vitesse est horizontal : sa composant verticale est nulle ; sa composante horizontale est 20 cosa .
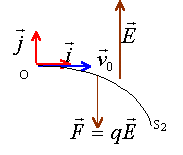
charge négative : les vecteurs champ et force électrique sont colinéaires de sens contraire.
Entre O et S2, la composante verticale de la vitesse augmente, alors que la composante horizontale de la vitesse reste constante. La norme du vecteur vitesse augmente et en conséquence l'énergie cinétique.
force centripète perpendiculaire au vecteur vitesse ( cette force n'effectue pas de travail et ne modifie pas l'énergie cinétique)
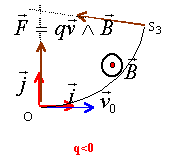
leurs normes sont égales : qvB = qE d'où vB=E.
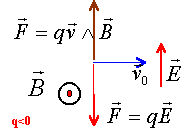
si les deux champs agissent et que la trajectoire est rectiligne alors les deux forces électrique et magnétique sont opposées
si arc de cercle alors champ magnétique
si arc de parabole alors champ électrique :
 |
|
coordonnées de la vitesse
accélération
énergies
|
On étudie le mouvement du centre d'inertie d'un mobile auto-porteur ,de masse m se déplaçant en translation sur un plan incliné d'un angle a par raport à l'horizontale.On lance le mobile vers le haut: Son centre d'inertie suit une trajectoire d'allure parabolique;le mobile rebondit sur l'élastique du bord inférieur de la table ,son centre d'inertie décrit une nouvelle trajectoire également d'allure parabolique.On désigne par t1 la date d'un instant situé peu avant le rebond, t2 la date d'un instant situé peu après le rebond. L' axe Ox est horizontal; l'axe Oy est dirigé suivant la ligne de plus grande pente du plan incliné et vers le haut.
Données : m=220g ; a=14,5° ; t1=0,53s ; t2=0,74s.
| t (s) |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
1,1 |
1,2 |
1,3 |
1,4 |
| x(m) |
0,04 |
0,055 |
0,07 |
0,092 |
0,11 |
0,125 |
0,14 |
0,16 |
0,17 |
0,18 |
0,19 |
0,2 |
0,21 |
0,22 |
0,23 |
- Quelle est la nature du mouvement horizontal de G avant la date t1? après t2?
- La valeur de la composante horizontale du vecteur vitesse avant la date t1 et après la date t2 reste-t-elle la même?
| t (s) |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
1,1 |
1,2
|
| vy(m /s) |
0,4 |
0,15 |
-0,1 |
-0,35 |
-0,6 |
-0,85 |
-0,7 |
0,55 |
0,6 |
0,35 |
0,1 |
-0,15 |
-0,4
|
- Que représente le coefficient directeur des courbes vy = f(t) .
- Déterminer ce coefficient et en déduire g ,intensité de la pesanteur.
- Déterminer les dates t3 et t4 pour lesquelles vy s'annule .Où se trouve alors le mobile?
- Donner les coordonnées des vecteurs vitesse et accélération aux dates t3, t4.
- Exprimer les énergies cinétique, potentielle et mécanique en fonction des grandeurs introduites dans les questions précédentes t, x, y, vx vy , m et a. L'énergie mécanique est différente avant t1 et après t2 .Que représente cette différence ?
- On garde la même inclinaison de la table et on lance, du même point, le mobile avec une vitesse initiale v'0 différente de v0 . Les données des deux tableaux ci dessus seront t'elles modifiées?Justifier.
- On change l'inclinaison de la table et on lance le mobile sans changer sa vitesse initiale .Même question.
corrigé
|
|
|
l'abscisse x croît d'environ 0,015 m lorsque le temps augmente de 0,1 s avant t1.
l'abscisse x croît d'environ 0,1 m lorsque le temps augmente de 0,1 s après t2.
abscisse et temps sont proportionnels.
la composante horizontale de la vitesse vx est constante.
Le mouvement est uniforme suivant l'axe des abscisses.
avant t1, vx = 0,015 / 0,1 = 0,15 ms-1.
après t2, vx = 0,01 / 0,1 = 0,1 ms-1.
l'ordonnée de la vitesse décroît d'environ 0,25 m s-1 lorsque le temps augmente de 0,1 s avant t1.
même remarque après t2.
ordonnée de la vitesse et temps sont proportionnels.
Le coefficient de proportionalité est une accélération : a = - 0,25/ 0,1 = 2,5 ms-2.
l'accélération d'un solide sur un plan incliné (frottement négligé) a pour norme g sina .
g sin 14,5 = 2,5 d'où g = 10 ms-2.
t3 voisn de 0,16 s et t4 voisin de 1,03 s.
Le mobile passe aux points les plus hauts de sa trajectoire.
| dates |
vitesse |
accélération |
| t3 |
vx= 0,15 ms-1.
vy=0
|
ax= 0
ay= -2,5 ms-2.
|
| t4 |
vx= 0,1 ms-1.
vy=0
|
ax= 0
ay= -2,5 ms-2.
|
aspect énergétique :
énergie potentielle : m g h = m g y sin a.
l'origine est prise sur le bord inférieur de la table inclinée.
énergie cinétique : 0,5 m(vx² + vy²)
énergie mécanique : m g y sin a + 0,5 m(vx² + vy²)
l'énergie mécanique ne se conserve pas lors du rebond sur le bord inférieur élastique.
La différence entre les 2 valeurs de l'énergie mécanique avant et après rebond est égale au travail des forces de contact élastique - solide.
si la vitesse initiale augmente ( angle a identique) :
les composantes horizontale et verticale de la vitesse varient, en conséquence l'abscisse x et l'ordonnée y varie dans le même sens que la vitesse.
Par contre l'accélération ne change pas, celle ci dépend de l'angle d'inclinaison et de g.
si l'angle d'inclinaison augmente( vitesse initiale identique en norme et sens) :
la composante horizontale de la vitesse ne change pas, en conséquence l'abscisse x ne change pas.
la composante vy dépend de l'angle d'inclinaison ( vy = -g sin a t + vy0), en conséquence vy change
|
fiche bac
- On étudie la propagation d'une perturbation le long d'une corde élastique. La figure 1 ci-dessous indique la forme de la perturbation qui se propage et les vecteurs vitesse VA et VB de deux points A et B de la corde à une date déterminée.
- Quel est le sens de propagation de la perturbation ? justifier la réponse.
- Ondes sonores et ondes radio :
On étudie la mise à feu de deux charges explosives situées en deux points A et B par un signal radio émis par un émetteur E ; L'observateur est situé au point O (la figure 2 ci-dessous donne les positions des différents points).L'observateur en O perçoit deux explosions. Quelle est la durée qui les sépare si :
- On suppose la propagation du signal radio quasi instantanée ?
- On tient compte de la célérité du signal radio ?
Données: Célérité du signal radio dans l'air : c=300 000km/s et celle du son dans l'air : v=330 m/s. AB=BE= 5km 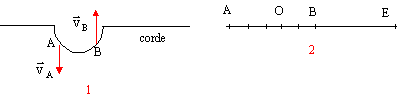
- La fondre est une décharge électrique frappant la Terre qui s'accompagne d'une émission lumineuse (l'éclair) et d'une émission sonore (le tonnerre). Soit d la distance séparant le lieu de l'orage de l'observateur ; on note Dt la durée séparant la perception du tonnerre de celle de l'éclair.
- Exprimer la distance d en fonction de v et de D t si on considère la propagation de la lumière comme pratiquement instantanée.
- Sans faire aucune simplification, exprimer la distance d en fonction de c, v et D t.
- Mettre l'expression de d sous la forme  = (vDt)/(1 - v/c ) = (vDt)/(1 - v/c )
- Montrer que le rapport v/c est nettement plus petit que 1 ; simplifier l'expression obtenu à la question c pour retrouver le résultat de la question a.
- Calculer la valeur de d pour D t=5,2 s.
Données : Célérité du signal radio dans l'air : c=300 000km/s et celle du son dans l'air : v=340 m/s.
corrigé
la déformation de la corde ou ébranlement est perpendiculaire à la corde .
la perturbation se propage suivant la direction de la corde.
l'explosion A est perçue à la date t1 = 3000 / 330 s
l'explosion B est perçue à la date t2 = 2000/330 s
t2-t1 = 1000 / 330 = 3,03 s
célérité du signal radio très supérieur à la célérité du son dans l'air : en conséquence le résultat précédent reste pratiquement inchangé.
d= v t1 ; d = c t2 d'où Dt = t1-t2 = d(1/v-1/c)= d(c-v)/(cv)
d = cvDt / (c-v) = vDt / (1-v/c) avec v/c = 340/3 108 = 1,1 10-6, négligeable devant 1.
d voisin de vDt = 340*5,2 = 1768 m.
|
|
simulation d'une hola :
La hola dans un stade peut être assimilée à une corde. Dans une classe, on effectue une simulation de hola.
- Un chemin a été défini pour la propagation de la hola.
- Chaque élève atteint par la hola effectue les opérations suivantes (soit d la distance entre deux élèves consécutifs) : a : il se lève ; b : il reste debout quelques instants ; c : il s'assoit.
- Un élève marque le rythme en prononçant fortement et régulièrement les lettres a, b, c.
- Quelques élèves observent et notent leurs commentaires.
- Propagation d'un hola unique.
A l'énoncé des lettres a, b, c, le premier élève effectue la suite des opérations, puis le deuxième ……
- Chaque élève a-t-il un mouvement périodique ?
- Que peut-on dire du mouvement d'un élève déterminé par rapport au mouvement du premier élève ?
- Propagation d'un hola périodique
L'élève continue à énoncer les lettres a, b, c mais à intervalles réguliers (abc, abc, abc,….), un signal est donné (par exemple par un coup de règle sur un table) et la hola repart du premier élève. Attention, chaque participant doit faire preuve de concentration et éviter de se tremper. On laisse progresser cette " hola périodique " et on l'arrête sur un b (marqué par un autre coup de règle), date où certains élèves sont debout (et restent debout).
- Chaque élève a-t-il un mouvement périodique ? Si oui, évaluer cette période T en fonction de la durée ta séparant deux a consécutifs.
- Lors de l'arrêt, observe-t-on une période spatiale ? Justifier la réponse.
- Lors de l'arrêt, quelle est la distance séparant deux élèves consécutifs qui sont debout ? Evaluer cette distance en fonction de l'intervalle entre deux élèves. Quelle grandeur mesure-t-on ainsi ?
- Quel temps met la hola pour parcourir la distance séparant deux élèves consécutifs qui sont debout ? Conclure.
corrigé
chaque élève se lève une seule fois, donc le mouvement ne se repète pas : mouvement non périodique.
l'élève de rang n reproduit le mouvement du premier avec un retard t.
Chaque élève a un mouvement périodique de période T= nta.
T : durée entre deux coups consécutifs de règle ( le premier se lève à nouveau)
n : nombre d'élèves entendant la lettre a et se levant entre deux coups de règle.
ta : durée entre deux "a "consécutifs.
Lors de l'arrêt on visualise la position debout ou assis de l'ensemble des élèves : photo de l'ensemble de la classe à une date donnée. Deux élèves consécutifs debout sont séparés par la distance "d" ( il y a une imprécision quand à la durée pendant laquelle les élèves restent debout).
|
|
mesure de la célérité du son :
Le son émis par le haut parleur est capté par deux microphones M1 et M2 branchés sur les voies YA et YB de l'oscilloscope. On voit deux courbes en phase ; chaque courbe représente deux périodes ; l'écran mesure 10 cm de large ; sensibilité 0,1 ms/cm.
- Calculer la fréquence du son capté par les microphones.
- Les abscisses x1 et x2 des deux microphones sont repérées sur la règle. Lorsque x1=x2=0 les courbes observées sur l'oscilloscope sont en phase. On laisse le microphone M1 en place et on déplace lentement le microphone M2. On relève l'abscisse x2 de ce microphone à chaque fois que les courbes sur l'oscilloscope sont de nouveau en phase. Les positions correspondantes sont données dans le tableau ci-dessous
| position n° |
1 |
2 |
3 |
4 |
5 |
| abscisse x2 (cm) |
17 |
34 |
51 |
68 |
85 |
-Quelle valeur de la longueur d'onde de l'onde sonore peut-on déduire de ces mesures ?
-Quelle est la célérité du son dans l'air à la température où sont effectuées les mesures ?
- Le son émis par le haut parleur est capté par le microphone M. On réalise les deux branchements sur l'oscilloscope ( haut parleur sur la voie 1 et microphone sur la voie 2)
- Quelles sont les deux tensions visualisées sur l'oscilloscope ?
- Quelle est la fréquence du son sachant que la rapidité de balayage est de 0,2 ms/cm ? (on observe deux périodes sur l'écran)
- On déplace le microphone M jusqu'à obtenir, sur l'écran de l'oscilloscope, deux sinusoïdes en phase. L'abscisse sur la règle est alors x1=4,5 cm. Puis on déplace le microphone le long de la règle ; la sinusoïde de la voie YB se décale alors progressivement par rapport à celle de la voie YA. Lorsque le microphone se trouve à l'abscisse x2=38,5 cm, les deux sinusoïdes se trouvent de nouveau en phase. Quelle est la valeur de la longueur d'onde de l'onde sonore dans l'air dans ces conditions ? Justifier la méthode. En déduire la célérité des ondes sonores dans l'air.
corrigé
Deux périodes correspondent à 10*0,1 = 1 ms soit T= 0,5 ms = 5 10-4 s.
fréquence = 1/T = 2000 Hz.
longueur d'onde : 17 cm = 0,17 m
célérité du son dans l'air : 0,17 / 510-4 = 340 m/s.
On visualise les tensions aux bornes du micro ( récepteur) et du haut parleur (source)
10*0,2 = 2 ms correspondant à 2 périodes
T= 1ms = 10-3 s et fréquence = 1000Hz.
les deux sinusoïdes se trouvent de nouveau en phase, le micro s'est déplacé d'une longueur d'onde :
x2-x1 = 38,5-4,5 = 34 cm = 0,34 m
célérité du son dans l'air : 0,34 / 1000 = 340 m/s.
|
|
diffraction par une fente
- Le laser hélum-néon émet une lumière rouge pratiquement monochromatique de longueur d'onde l=633nm. Une fente de largeur a est placée sur le trajet du faisceau lumineux produit par le laser. Un écran est placé à la distance D=2,50 m de la fente. On déplace une cellule photoélectrique le long de l'axe x'x (O est le point d'incidence du faisceau en l'absence de fente). Cette cellule est alors une source de tension u proportionnelle à l'intensité lumineuse en chaque point M de l'axe x'x, d'abscisse OM=x.
| x
mm
|
+/-26 |
+/-24 |
+/-22 |
+/-20 |
+/-18 |
+/-16 |
+/-15 |
+/-14 |
+/-13 |
+/-12 |
+/-11 |
+/-10 |
+/-9 |
+/-8 |
+/-7 |
+/-6 |
+/-5 |
+/-4 |
+/-2 |
+/-0 |
| u(V) |
0,2 |
0,1 |
0 |
0,2 |
0,6 |
0,7 |
0,6 |
0,5 |
0,2 |
0 |
0,2 |
0,7 |
1,3 |
2 |
2,4 |
3,3 |
3,8 |
4,3 |
4,7 |
4,8 |
- Tracer la courbe représentant les variations de la fonction u=f(x), pour les valeurs de x comprises entre -26 mm et + 26 mm. Interpréter l'allure de la courbe précédente.
- La largeur l de la tache centrale de la figure de diffraction observée sur l'écran est : l=2lD/a .Evaluer alors la largeur a de la fente.
corrigé
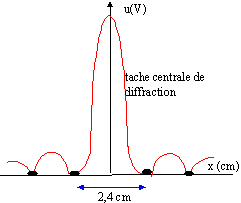
l = 2,4 10-2 m
diffraction : on observe une tache centrale brillante et de part et d'autre une alternance de taches sombres et de taches de moins en moins brillantes.
a = 2lD / l =2*6,33 10-7 * 2,5 / 2,4 10-2 = 1,32 10-4 m.
|
|
diffraction d'ondes :
- Une source lumineuse monochromatique, de longueur d'onde l, et ponctuelle est placée devant une fente de largeur a, sur l'axe de cette fente, à la distance d=20cm de la fente. Un écran se trouve à la distance D=50cm derrière la fente.
- Déterminer la largeur de la zone éclairée de l'écran (dans la direction perpendiculaire à SA) dans les deux cas suivants : l =600 nm et a=4,0 cm ; l =600 nm et a=0,10 mm.
- Un haut parleur est placé devant une large planche percée d'une fente de largeur a=3,0 cm, dans l'axe de la fente. Le haut parleur est branché sur un générateur basse fréquence réglé sur la fréquence f=500 Hz.
-Y a-t-il diffraction des ondes sonores à la traversée de la fente ? Justifier la réponse.
- Si oui, comment le phénomène se manifeste-t-il ?
- Derrière la fente, on place un microphone dont on relie les bornes à l'entrée YA d'un oscilloscope réglé sur la rapidité de balayage 1 ms/div. Faire le schéma de l'écran de l'oscilloscope sachant que, horizontalement, il comporte 10 divisions. On justifiera tous les points du raisonnement.
- Qu'observe-t-on en déplaçant le microphone :+
* En restant à la même distance de la fente ?
* En s'éloignant de la fente ?
Données :Célérité des ondes sonores dans l'air : v=340m/s.
corrigé
si a = 4cm il n'y a pas de diffraction, car la largeur de la fente n'est pas du même ordre de grandeur que la longueur d'onde de la lumière (600 nm = 0,6 mm)
on note L le rayon de la tache : Thalès donne L/a = (D+d) / d
L = a(D+d) / d = 4 10-2 * 0,7/0,2 = 0,14 m.
si a = 10-4 m il y a diffraction, on note L la largeur de la tache centrale :
L = 2l D/a = 2 *6 10-7 *0,5 / 10-4 = 6 10-3 m.
longueur d'onde : 340 / 500 = 0,68 m
3 cm et la longueur d'onde sont du même ordre de grandeur, donc diffraction des ondes sonores par la fente.
La fente se comporte comme une source sonore émettant au dela de la fente dans toutes les directions :
* en déplaçant le microphone sur un arc de cercle centré sur la fente, on observe que l'amplitude de l'onde reste constante.
* en éloignant le microphone de la fente on observe une diminution de l'amplitude de l'onde.( perte d'énergie)
Relier la masse du microphone à la masse de l'oscilloscope et l'autre fil issu du micro à l'une des entrées de l'oscilloscope.
période de l'onde T= 1/500 = 2 ms
largeur de l'écran : 10 cm ; sensibilité 1 ms/cm soit 10 ms pour toute la largeur de l'écran
on observe alors 5 périodes.
|
|
Un pointeur optique à laser a la forme et la taille d'un gros stylo. Le faisceau lumineux qui en sert, lorsqu'il est dirigé en direction d'un tableau, donne un point d'impact rouge très lumineux et de petites dimensions. Il permet à un conférencier, même lorsqu'il se trouve très loin du tableau, de pointeur un endroit précis d'un document projeté. On veut retrouver expérimentalement l'ordre de grandeur de la longueur d'onde l0 de la lumière émise par le pointeur optique à laser (longueur d'onde indiquée dans la fiche technique : l0 comprise entre 660 et 680nm ).
On utilise le montage suivant : une fente verticale, de largeur a très petite, est placée sur le trajet du faisceau lumineux produit par le laser et un écran est placé à la distance D de la fente.
- Recopier la phrase suivante en la complétant : " Le phénomène qui se manifeste s'appelle ……. ; son importance est liée au rapport de la largeur a de la fente à ……… ".
- On propose quatre expressions pour la largeur l de la tache centrale :
(a) : l= (2lD)/a (b) : l= 2aD/l (c) : l= 2D2/la (d) : l= (2la)/D
et on réalise trios expériences :
| expérience |
source |
distance D |
largeur a |
largeur tache centrale l |
| n°1 |
source l1= 543 nm |
D |
a |
l1=3,2 cm |
| n°2 |
source l0 |
D |
a |
l2=4 cm |
| n°3 |
source l1= 543 nm |
D |
a3 < a |
l3>l1. |
- Par une analyse dimensionnelle, montrer qu'une des expressions est manifestant fausse.
-A partir des expériences, déterminer les autres expressions que l'on doit éliminer (on précisera à chaque fois les expériences prises en compte). En déduire l'expression de la largeur l de la tache centrale.
- Etablir la relation entre l1, l2, l1 et l0. Calculer avec le bon nombre de chiffres significatifs, la valeur numérique de l0. Ce résultat est-il en accord avec la notice technique du pointeur optique à laser ?
corrigé
" Le phénomène qui se manifeste s'appelle diffraction ; son importance est liée au rapport de la largeur a de la fente à la longueur d'onde ".
dans les expressions proposées, les différents paramètres sont des longueurs en mètre :
(c) est fausse car D2a/l est homogène au carré d'une longueur.
expériences n°1 et n°2 : l1 <l0 et l1<l2 donc longueur d'onde et largeur de la tache centrale de diffraction sont proportionnelles ( si a et D constants)
en conséquence (b) est fausse.
expériences n°1 et n°3 (l1 constante, inchangée ) : a3<a et l1<l3 donc largeur de la fente et largeur de la tache centrale de diffraction sont inversement proportionnelles ( si D et l1 constants)
en conséquence (d) est fausse.
(a) vrai : l= (2lD)/a
l1 / l1 = l2 / l0= 2D/a soit l0= l1 l2 /l1 = 543*4/3,2 = 678 nm.
|
| dipôle RC : charge d'un condensateur ; bilan énergétique
On considère le circuit suivant comprenant, montés en série : un générateur de tension continue de fem E=6 V et de résistance interne nulle, une résistance R=5 kW, un condensateur de capacité C=1,2mF et un interrupteur K.
Etude de la charge :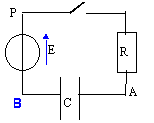
- Préciser sur le schéma du montage, le sens positif choisi pour l'intensité du courant i.
- Etablir l'équation différentielle de charge liant la tension instantanée uAB(t) aux bornes du condensateur et sa dérivée par rapport au temps duAB/dt en fonction de R, C et E.
- Vérifier que l'expression uAB(t) = E(1-e-t/(RC)) est solution de l'équation différentielle trouvée précédemment. La tension initiale du condensateur uAB(t=0)=0 est-elle compatible avec les données de l'exercice ? Quelle est la valeur maximale que peut atteindre la tension uAB(t) ?
- Donner la dimension du produit RC. Comment appelle-t-on ce produit ? Quelle est sa signification pratique pour ce circuit ?
- Calculer la valeur de la tension instantanée aux instants t=5 ms, t=10 ms, t=20 ms et t=50 ms.
- Tracer l'allure de la tension uAB(t)
- Déterminer l'expression de l'intensité du courant i(t) en fonction du temps t et des paramètres E, R et C. Calculer sa valeur numérique à l'instant t=0.. Lorsque t est très grand, que vaut l'intensité du courant ?
Bilan énergétique :
- Quelle est l'expression, en fonction de E et C de l'énergie électrique WC emmagasinée dans le condensateur lorsque la charge est terminée ?
- La puissance électrique instantanée délivrée par le générateur est p(t) = dWel /dt = Ei(t). Déterminer l'énergie électrique totale Wel délivrée au circuit par le générateur au cours de la charge en fonction de E et C.
- Déduire des deux questions précédentes l'expression WR, de l'énergie dissipée dans la résistance R au cours de la charge.
corrigé
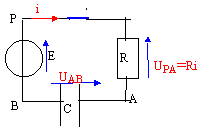
uPB= E ; uPB= uPA+ uAB avec i = dqA/dt = CduAB/dt .
E= Ri +uAB soit E=RC duAB/dt +uAB (1)
dériver l'expression de uAB par rapport au temps : duAB/dt = E/(RC) e-t/(RC).
repport dans (1) : E= RC*E/(RC) e-t/(RC)+E(1- e-t/(RC))
E = Ee-t/(RC) + E-E e-t/(RC) égalité vérifiée.
uAB (t=0)= E(1-e0) = E(1-1)=0 condensateur initialement non chargé.
uAB (t=oo)= E(1-0) =E condensateur entièrement chargé.
t =RC = 5 103*1,2 10-6 = 5 10-3s = 5 ms constante de temps en seconde. Au bout de 5t le condensateur est considéré comme chargé.
| t = 5ms |
t=10 ms |
t= 20 ms |
t= 50 ms |
| uAB =6(1-0,37) =3,78 V |
uAB= 4,87 V |
uAB= 5,78 V |
uAB= 6 V |
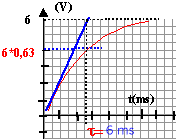
i = CduAB/dt = C E/(RC) e-t/(RC)= E/R e-t/(RC).
à t=0 l'intensité vaut : 6/5000 e0 = 6/5000 = 1,2 mA.
au bout d'un temps infini l'intensité est nulle.
énergie stockée par le condensateur chargé : WC= ½CE²
énergie fournie par le générateur :
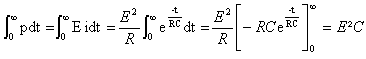
Wel = WC+WR d'où WR= ½CE²
|
| mouvement du centre d'inertie d'une mini-fusée
Dans un club amateur, on étudie la trajectoire d'un modèle réduit de fusée. La fusée pourra être considérée comme une masse ponctuelle M ramenée en son centre d'inertie et on ne tiendra pas compte de la résistance de l'air.
Dans un premier temps, la fusée est lancée horizontalement depuis un point O, à une date t=0, avec un vecteur initial v0, dans un domaine limité où le champ de pesanteur est uniforme et a pour intensité g0 = 9,81 m/s². On étudie le mouvement du centre d'inertie de la fusée dans un repère terrestre (Ox,Oz), Ox est l'axe horizontal de même sens et direction que la vitesse initiale. Oz est l'axe vertical orienté vers le bas.
- Exprimer le vecteur accélération de la fusée dans le repère choisi.
- Etablir sous forme littérale, les équations exprimant les coordonnées x(t) et z(t) de la fusée en fonction du temps lors du mouvement dans le repère choisi.
- En déduire l'expression littérale de la trajectoire de la fusée.
- Déterminer numériquement les coordonnées de la fusée à la date t=2s si v0=5 km/s.
Dans un second temps, au sommet du mont Everest de hauteur h, on fait décrire à la fusée une orbite circulaire, dont le centre est le centre de la terre, en lui donnant une vitesse suffisante v1. L'expression du champ de pesanteur à l'altitude h est donné par : g = g0 R² / (R+h)² avec R= 6,38 106 m
- Que peut-on dire du vecteur accélération de la fusée ? En déduire que son mouvement est uniforme de vitesse v1.
- Etablir l'expresion littérale de la vitesse v1 de la fusée en fonction de g0, h et R.
- Calculer la valeur de v1 si h = 8,85 103 m.
- Quelle est la valeur numérique de la période T du mouvement de la fusée ?
corrigé
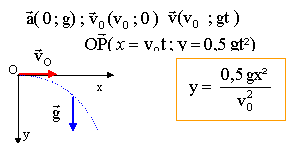
x(t=2) = 5000*2 = 104 m ; y(t=2) = 0,5 *4*9,8 = 19,6 m.
La fusée n'est soumise qu'à la force de gravitation de la terre, force centripète; cette force est perpendiculaire à la vitesse; en conséquence elle ne travaille pas et ne modifie pas l'énergie cinétique. Donc la valeur de la vitesse est constante et le mouvement est uniforme.
a=g0R²/ (R+h)² = v1² / (R+h) d'où v1² = g0R²/ (R+h)
v1² =9,8(6,38 106)² / (6,38 106 + 8,85 103) = 62,43 106 soit v1 = 7,9 103 m/s.
La circonférence de rayon (R+h) est parcourue à la vitesse v1 durant une période T
2p(R+h)=v1T soit T= 2p(R+h)/v1
T= 6,28*(6,38 106 + 8,85 103) / 7,9 103 = 5 103 s.
|
transformations nucléaires
L'iode 131 13153I est un radionucléide ayant la propriété de se fixer sur la glande thyroïde. Il présente une radioactivité de type b-.
- Donner la composition du noyau d'iode 131.
- Lors de la désintégration b-, quelle transformation se produit dans le noyau d'iode 131 ? Ecrire l'équation de cette transformation.
- Ecrire l'équation de la réaction de désintégration b- de l'iode 131 et préciser les lois de conservation utilisées.
Antimoine Sb: Z= 51 ; tellure Te Z=52 ; Xénon Xe Z=53 ; Césium Cs Z=55.
- Une personne a été contaminée par de l'iode 131 dont le temps de demi-vie ou période est T=8 jours.
- Définir en une phrase le mot demi-vie.
- Le nombre N(t) de noyaux non désintégrés au bout d'un temps t est donné par N(t) = N0 e-lt où N0 est le nombre de noyau d'iode 131 à l'instant t=0 et l une constante radioactive. Déterminer l'expression de la constante radioactive l en foncrtion de la période T et calculer sa valeur numérique.
- Pour la personne contaminée à l'instant t=0, calculer le temps au bout duquel il ne restera plus que 1/126 ème du nombre de noyaux d'iode 131 initial fixés sur la glande thyroïde.
corrigé
53 protons et 131-53 = 78 neutrons
un neutron se transforme en proton : 01n-->11p + -10e
13153I --> AZX + -10e
conservation de la charge : 53=Z-1 d'où Z=54 élément Xe
conservation du nombre de nucléons : 131=A+0.
Le temps de demi-vie ou période est la durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés.
à t=T, N(T)=½ N0= N0e-lT
soit 0,5 = e-lT ou ln2 = lT ; l =ln2 / T = 0,693 / 8 = 0,0866 jour-1.
128 est égal à 27 donc au bout de 7 périodes ou 56 jours le nombre de noyaux initial est divisé par 128.
|
réaction entre l'éthanol et le sodium pur
- Dans 30 mL d'étanol on introduit 1 g de sodium. La réaction qui se produit est assez vive et donne des ions éthanolate CH3CH2O-, des ions sodium Na+ et du gaz dihydrogène H2.
a- Ecrire l'équation chimique de la réaction entre l'éthanol et le sodium.
b- Montrer que tout le sodium a réagi.
c- En déduire le nombre de moles d'ion éthanolate formés au cours de la réaction.
- Après refroidissement du mélange réactionnel, on le verse dans une fiole jaugée de 200 mL et on complète avec de l'eau disssstillée. La solution ainsi obtenue est appelée S, son volume est noté V.
a- L'ion éthanolate étant une base, écrire l'équation chimique de la réaction des ions éthaolate avec les molécules d'eau.
b- On donne v= 10 mL de solution S par une solution d'acide chlorhydrique de concentration Ca = 0,2 mol/L. L'équivalence acido-basique est obtenue lorsqu'un volume va = 10,7 mL d'acide a été ajouté. Montrer que ce résultat est en accord avec la réponse obtenue en 1c. Justifier.
masse atomique molaire (g/mol) Na=23 ; C=12 ; H=1 ; O=16.
masse volumique de l'éthanol r =790 kg/m3.
corrigé
CH3CH2OH + Na -->CH3CH2O- + Na+ +½H2.
Quantité de matière initiale :
sodium 1/23 = 0,0435 mol
éthanol : 30*0,79 = 23,7 g puis 23,7 / (12*2+6+16) =0,515 mol
l'éthanol est en excès, le sodium en défaut.
il se forme donc 0,0435 mol d'ion éthanolate et 0,0435 mol éthanol a réagi. CH3CH2O- + H2O-->CH3CH2OH+HO-
à l'équivalence du dosage acide base : CaVéqui = [HO-] v soit 0,2*10,7 = 2,14 mmol d'ion HO- dans 10 mL de S
soit 2,14*200 /10= 42,8 mmol d'ion HO- ( ou d'éthanol) dans 200 mL de S
0,0428 mol éthanol a réagi avec le sodium
résultat très proche de 0,0435 mol trouvé ci-dessus.
|
oxydo-réduction et catalyse
- Dans une solution d'iodure de potassium (K+ ; I-) on verse une solution de peroxodisulfate de sodium ( 2Na+ ; S2O82-). La réaction est théoriquement possible mais on n'observe rien. Expliquer pourquoi.
- On ajoute quelques cristaux de sulfate de fer II FeSO4. On observe alors un changement de couleur de la solution. Une analyse montre que la concentration en ions Fe2+ n'a pas varié après la réaction.
a- Expliquer le processus ayant conduit à ce changement de couleur.
b- Ecrire les équations chimiques des réactions qui se sont produites. Quel est le rôle joué par les ions Fe2+?
couples oxydant/ reducteur : S2O82-/ SO42- ; I2/I- ; Fe3+/ Fe2+.
corrigé
On n'observe rien car la réaction est lente à 20°C.
Le catalyseur Fe2+ accélére la réaction: une réaction lente est remplacée par deux réactions rapides.
S2O82-+2e-= 2SO42- réduction
2Fe2+= 2Fe3+ + 2e- oxydation
S2O82-+2Fe2+-->2SO42- +2Fe3+ oxydo-réduction rapide.
2I-= I2+ 2e- oxydation
2Fe3+ + 2e- =2Fe2+ réduction
2I- +2Fe3+--> I 2+2Fe2+ rapide, le catalyseur est régénéré.
|
radioactivité
- L'iode intervient dans le métabolisme de la glande thyroide. L'iode 127 ( 12753I) est stable alors que l'iode 131 est émetteur b+ et l'iode 124 est émetteur b-.
Données : m(iode 131) = 130,87697 u ; m(proton)= 1,007270023 u ; m(neutron) = 1,008665842 u ; c=3 108 m/s ; 1u = 1,66054 10-27 kg ; 1 eV= 1,602 10-19 J.
Quelle est l'énergie de liaison (MeV) du noyau d'iode 131 ?
11 ; 170 ; 110 ; 1705 ; 1103 ; 17.
- Le cobalt 60 utilisé en radiothérapie est un émetteur b- dont le schéma de désintégration est donné ci dessous :
Ni*: noyau de nickel excité 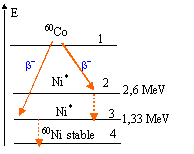
Données : h= 6,62 10-34 Js.
Quelle est la longueur d'onde (m) de l'émission qui se produit lors de la transition du niveau 3 au niveau 4 ?
1,65 10-12 ; 9,32 10-7 ; 1,65 10-6 ; 9,32 10-13 ; 3,22 10-9 ; 3,22 10-13.
corrigé
53 protons et 131-53 = 78 neutrons
défaut de masse : 53*1,007270023 + 78*1,008665842-130,87697 = 1,184427 u
1,184427*1,66 10-27 = 1,9659 10-27 kg.
énergie : Dmc² = 1,9659 10-27 *(3 108)² = 1,77 10-10 J
1,77 10-10 / 1,6 10-19 = 1,106 109 eV = 1106 MeV.
E=hc/l soit l = E/(hc)
E = 1,33 MeV = 1,33 106 eV = 1,33 106 *1,6 10-19 J= 2,128 10-13 J
l = 2,128 10-13/ (6,62 10-34 * 3 108) = 9,33 10-13 m.
|
| ondes
- Une radiation rouge a pour longueur d'onde dans le vide l =656,3 nm. Pour cette radiation, l'indice du verre est n=1,612. c=3 108 m/s.
- Quelle est sa fréquence (Hz) ?
197 ; 4,57 1014 ; 2,19 10-15 ; 1,52 109 ; 4,57 1011 ; 2,19 1014.
- Quelle est la célérité (m/s) de cette radiation dans le verre ?
3 108 ; 4,84 108 ; 2,52 108 ; 1,86 108 ; 1,47 108 ; 2,25 108 ;
- Sur une canalisation en acier dans laquelle circule de l'eau, on provoque un choc. Un capteur situé à une distance d, détecte deux signaux sonores, brefs, séparés par une durée égale à 1,8 s ; célérité du son dans l'acier : 5 km/s; célérité du son dans l'eau 1,5 km/s.
- Quelle est la distance d(m)
3,87 ; 51 ; 3857 ; 1,94 ; 0,51 ; 194.
- Le quartz d'une montre A, parfaitement réglée, vibre à la fréquence f0 = 32768 Hz. Une autre montre à quartz B, identique à A, retarde de 2 s par semaine par rapport à A
- Quel est l'écart de fréquence (Hz) de vibration des deux quartz ?
1 ; 10 ; 3,3 10-6 ; 7 ; 0,1 ; 0,7.
corrigé
f= c/l = 3 108 / 656,3 10-9 = 4,57 1014 Hz.
indice n = 3 108 / célérité dans le verre
célérité dans le verre = 3 108 / n = 3 108 /1,612 = 1,86 108 m/s.
dans l'eau, la durée du parcours de l'onde est : t1 = d/ve = d/1500 s
dans l'acier, la durée du parcours de l'onde est : t2 = d/va = d/5000 s
t = t1 - t2 =d( 1/1500-1/5000) = 4,66 10-4 d.
d =t / 4,66 10-4 = 1,8 / 4,66 10-4 =3862 m.
période T0 = 1/32768 = 3,0517578 10-5 s.
pour que la montre affiche une seconde il faut amplifier, multiplier T0 par 32768.
retard : 2/7 = 0,2857 s /jour ; 0,2857 / 24 = 0,0119 s/heure; 0,0119 / 3600 = 3,307 10-6 s à chaque seconde.
en tenant compte du coefficient d'amplification on trouve la période T :
T = T0+3,307 10-6 / 32768 =T0+10-10 = 3,0517678 10-5 s.
puis la fréquence f = 1/T = 32767,9 Hz soit un écart de 0,1 Hz.
|
circuit RC, RL, RLC
- Une bobine idéale d'inductance L= 1,5 mH est branchée en série avec une résistance R= 100 ohms et un générateur de tension continue, de fem E=9 V. A t=0, l'interrupteur est fermé.
- Quelle est la valeur de la constante de temps t du circuit ( seconde) ?
1,5 10-5 ; 0,15 ; 66,7 ; 150 ; 6670 ; 3,87 10-2.
- Que vaut la tension (V) aux bornes de la bobine à t= 5t.
9 ; 5,7 ; 3,3 ; 4,5 ; 2,1 ; 0
- Que vaut l'intensité du courant (mA) à t= 1 ms.
11,1 ; 21 ; 90 ; 57 ; 0 ; 45.
- Un circuit oscillant non amorti, comporte une bobine d'inductance L=0,1 H et un condensateur de capacité C=2,2 mF. Le condensateur est initialement chargé sous une tension de 12 V.
- Quelle est l'énergie maximale (J) emmagasinée par la bobine ?
1,32 10-4 ; 3,17 10-4 ; 1,6 10-4 ; 0,6 ; 0,8 10-4 ; 2,1 10-3 .
- Quelle est l'intensité (A) maximale du courant dans le circuit ?
0,2 ; 5,6 10-2 ; 1,6 10-3 ; 4 10-2 ; 0,45 ; 5,7 10-3 .
corrigé
constante de temps t = L/R = 1,5 10-3 /100 = 1,5 10-5 s.
après une durée supérieure à 5t, le régime permanent est établi et la tension aux bornes de la bobine est égale à zéro si sa résistance est nulle.
à t = 10-3 s, valeur supérieure à 5t, le régime permanent est établi et l'intensité vaut : i = E/R = 9/100 = 0,09 A = 90 mA.
l'énergie maximale stockée par le condensateur se retrouve dans la bobine si la résistance du dipôle est nulle .
E = ½Cu² = 0,5 *2,2 10-6 *12² = 1,584 10-4 J.
intensité maximale : E=½Li² soit i² = 2E/L =2*1,584 10-4 / 0,1 = 3,168 10-3 soit I = 0,056 A.
|
| chute, satellite, oscillateur
- Une boule de bois de rayon 6,4 cm tombe verticalement dans l'air. La force de résistance due à l'air est de la forme
fr = -r0 S Cx v²
Données : masse volumique du bois :rb =620 kg/m3 ; Cx=0,45; S section de la boule.masse volumique de l'air :r0 =1,21 kg/m3 ;
- Quelle est la valeur de la vitesse limite (m/s) atteinte par la boule ?
4,4 ; 19,1 ; 25,1 ; 13,7 ; 34,2 ; 43,7
- Un satellite de type SPOT a une trajectoire circulaire surplombant les poles terrestres. Il s'agit d'un satellite dit à défilement, destiné à fournir des images de tout le globe terrestre. La période de passage au dessus d'un même lieu est égale à 26 jours solaires moyens et correspond à la durée de 369 révolutions du satellite.
Données : rayon de la terre RT= 6380 km ; masse de la terre MT= 5,98 1024 kg ; constante de gravitation G= 6,67 10-11 Nm² kg-2 ; durée du jour solaire moyen : 86400 s.
- Quelle est la période (s) de révolution du satellite ?
6088 ; 1,23 106 ; 11,1 ; 9 ; 3044 ; 12176.
- Quelle est l'altitude (km) du satellite ?
65698 ; 830 ; 7210 ; 35800 ; 27600 ; 4220.
- Dans un manuel d'apprentissage du tennis on peut lire le conseil suivant concernant le service "Frappez la balle devant vous de façon à donner à la balle une vitesse en dessous de la direction horizontale ". Un tennisman frappe la balle à une hauteur h=2,4 m . Le vecteur vitesse de la balle dirigé vers le bas, fait un angle a=10° avec l'horizontale et a une valeur v0=30 m/s.
- Quelle est la vitesse (m/s) de la balle en touchant le sol ?
29,2 ; 47 ; 58 ; 34,3 ; 30,8 ; 41,7.
- Dans un bâtiment public, un lustre assimilable a un pendule simple, oscille régulièrement. La durée de 10 oscillations est de 49,2 s.
- Quelle est la longueur( m) du câble auquel est suspendu le lustre ?
6 ; 7,7 ; 37,7 ; 12,2 ; 4,3 ; 8,6.
- Un oscillateur élastique horizontal est constitué d'un solide de masse m=256 get d'un ressort hélicoïdal à spires non jointives de raideur k= 78 N/m.
- Quelle est la période propre (s) de l'oscillateur ?
11,38 ; 3,47 ; 0,02 ; 1,91 ; 0,71 ; 0,36.
Quelle est la valeur (rad) de la phase à l'origine ?
p/4 ; p ; 3p/2 ; p/2 ; 0 ; 3p/4.
- Quelle est la valeur de la vitesse (m/s) lorsque l'élongation est x=0,5 cm ?
2,2 10-2 ; 0,34 ; 0,26 ; 8,7 10-2 ; 0,12 ; 0,17.
- Un athlète a parcouru un 100 m en 10,5s. On modèlise sa course e considérant 2 phases : il accélère uniformément pendant les 15 premièrs mètres de course, qu'il parcourt ensuite à vitesse constante de 10 m/s jusqu'à l'arrivée.
- Quelle est la valeur de l'accélération moyenne (m/s²) pendant la phase de démarrage ?
0,95 ; 0,12 ; 9,5 ; 5 ; 6,7 ; 4,3.
corrigé
lorsque la vitesse limite est atteinte le mouvement est rectiligne uniforme. La valeur du poids de la boule est égale à la valeur de la force de frottement.
volume de la boule = 4/3 pr3 ;
masse = volume * masse volumique du bois =4/3 pr3 rb ; poids = 4/3 pr3 rb g
frottement = r0 S Cx v²lim ; avec S = pr2.
4/3 pr3 rb g = r0 pr2 Cx v²lim d'où 4/3 r rb g = r0 Cx v²lim et v²lim =4r rb g /(3r0 Cx )
v²lim = 4*6,4 10-2 *620*9,8 / (3*1,21*0,45)=952 soit vlim = 30,8 m/s.
période : 26*24*3600 / 369 = 6088 s.
3ème loi de Kepler : T² / r3 = 4p² / (GM)
4p² / (GM) =4*3,14² / (6,67 10-11 *5,98 1024) = 9,88 10-14.
r3 = T² / 9,88 10-14 = 6088² /9,88 10-14 = 0,375 1021 soit r = 0,721 107 m = 7210 km
il faut retrancher le rayon de la terre h = 7210-6380 = 830 km.
théorème de l'énergie cinétique : seul le poids travaille (mgh)
½mv²-½mv0² = mgh soit v² = v0² +2gh = 900 + 2*9,8*2,4 = 947 et v = 30,78 m/s.
période T= 4,92 s. Or T = 2p racine carrée (l/g)
T² = 4p² l/g soit l = T²g/ (4p² ) = 4,92² *9,8 / (4*3,14²) = 6 m.
T = 2p racine carrée (m/k) = 6,28 [0,256 / 78]½ = 0,36 s.
x(t) = 0,02 cos (wt) avec w = 2p/T = 6,28 / 0,36 = 17,44 rad/s.
la phase initiale est nulle.
à quelle date t, l'élongation vaut-elle 0,005 m ?
0,005 = 0,02 cos( 17,44 t) soit cos(17,44t)= 0,005/0,02 = 0,25 = cos( 1,318 ) ( angle en radian)
t = 1,318 / 17,44 = 0,07555 s.
la vitesse est la dérivée de x(t) par rapport au temps : v(t) = 0,02 w (-1) sin( wt)
|v(t)| = 0,02*17,44 sin (1,318) = 0,02*17,44 * 0,9682 = 0,34 m/s.
durée du mouvement rectiligne uniforme : (100-15) / 10 = 8,5 s
durée de la phase de démarrage Dt =10,5/8,5 = 2s
variation de la vitesse au cours du démarrage : D v = 10 m/s
accélération moyenne a = D v /Dt = 10/2 = 5 m/s².
|
acide base
- Le taux d'avancement final, d'un volume v0=100 mL de solution d'acide méthanoïque (HCOOH) de concentration initiale c0=0,1 mol/L est 0,04. Quel est le pH de la solution ?
1,6 ; 1,4 ; 2,4 ; 3,4 ; 4,4 ; 3.
- A la date t=0, on introduit dans un bécher un volume v=30 mL d'une solution aqueuse contenant des ions peroxodisulfate S2O82-, de concentration c=0,1 mol/L et un volume v'=40 mL d'une solution aqueuse contenant des ions iodures I- de concentration c=0,1 mol/L. La réaction est lente ; il se forme du diiode et des ions sulfates SO42-. Le dosage du diiode formé au cours du temps fournit les mesures suivantes :
| t(s) |
0 |
20 |
40 |
60 |
80 |
100 |
120 |
200 |
| nI2 10-4 mol |
0 |
4,4 |
7,7 |
10,7 |
12,6 |
14,2 |
15,8 |
18,2 |
- Quel est l'ordre de grandeur de la vitesse volumique de la réaction à l'instant initial (mol L-1 s-1)
3,6 10-4 ; 1,8 10-4 ;7,2 10-4 ;9,2 10-4 ; 8,3 10-4 ; 1,2 10-3.
- Quel est le temps de demi-réaction ? (s)
30 ; 120 ; 200 ; 55 ; 90 ; 250.
- On mesure la résistance à 25°C d'une solution aqueuse d'acide propanoïque de concentration c0=3 10-3 mol/L. On trouve R= 12 kW. Les plaques de la cellule de conductimètrie ont une surface de 1,1 cm² et sont distantes de 1 cm. l(CH3-CH2-COO-) = 3,6 10-3 ; l(H3O+) = 3,5 10-2 Sm²mol-1.
- Quelle est la valeur de la constante d'acidité Ka de cet acide ?
2,2 10-2 ; 6,3 10-10 ; 4,5 10-7 ; 7,6 10-3 ; 1,3 10-3 ; 8,9 10-2 .
corrigé
[H3O+]= t c0 = 0,04*0,1 = 4 10-3 mol/L
pH = -log(4 10-3 ) = 2,4.
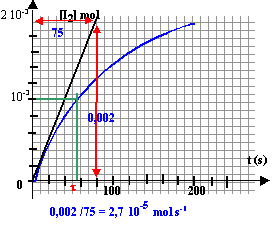
v0 = 1/V dnI2/dt = 1/((30+40) 10-3)*2,7 10-5= 3,8 10-4 mol L-1 s-1.
Quel est le réactif limitant ?
S2O82- + 2e- = 2SO42-
2I-=I2+2e-
S2O82- + 2I- = 2SO42- +I2.
|
|
S2O82- |
+ 2I- |
= I2 + .... |
| initial |
0,03*0,1 = 3 10-3 mol |
0,04*0,1 = 4 10-3 |
0 |
| en cours |
3 10-3 -x |
4 10-3 -2x |
x |
| fin |
3 10-3 -xmax |
4 10-3 -2xmax |
xmax |
4 10-3 -2xmax donne xmax =2 10-3 mol ; 3 10-3 -xmax =0 donne xmax =3 10-3
ion iodure en défaut : t½ , date à laquelle la moitié du réactif limitant a disparu.
t½ correspond à x = ½ xmax = 10-3 mol I2 ; la lecture sur le graphe donne t½ voisin 55 s.
R= 12000 W ; conductance G=1/R = 1/12000 = 8,33 10-5 S.
constante de cellule : k = d/S = 0,01 / 1,1 10-4 = 90,9 m-1.
conductivité s = kG = 90,9 *8,33 10-5 = 7,57 10-3 Sm-1.
CH3-CH2-COO H + H2O=CH3-CH2-COO-+H3O+
[CH3-CH2-COO-] =[H3O+]= t c0 ; [CH3-CH2-COO H ]=(1-t )c0
s =[l(CH3-CH2-COO-) + l(H3O+) ] t c0 ; avec c0 = 3 10-3 *103 = 3 mol/m3.
t =s / [[l(CH3-CH2-COO-) + l(H3O+) ] c0 ] = 7,57 10-3 / [(35+3,6)10-3*3]=0,065.
Ka = [CH3-CH2-COO-] [H3O+] / [CH3-CH2-COO H ] = t² c0 / (1-t ) = 0,065² *3 10-3 / (1-0,065) = 1,36 10-5.
|
ester
- Le benzoate de méthyle, à odeur d'oeillet, est utilisé en parfumerie. Pour le synthétiser, on chauffe à reflux, sous la hotte pendant environ une heure 12,2 g d'acide benzoïque C6H5COOH, 40 mL de méthanol et 3 mL d'acide sulfurique. Après refroidissement du mélange réactionnel, on verse celui-ci dans une ampoule à décanter contenant 50 mL de solution saturée de chlorure de sodium. Après séparation des deux phases, lavage, séchage de la phase organique , on récupère par distilation une masse finale mf=10,2 g de benzoate de méthyle.
| composé |
acide benzoïque |
méthanol |
benzoate de méthyle |
| M(g/mol) |
122 |
32 |
136 |
| m(g/cm3) |
1,321 |
0,791 |
1,089 |
Quel est le rendement de cette synthèse ?
60 % ; 30 % ; 100 % ; 25 % ; 50 % ; 75 %.
- La réaction entre l'acide butanoïque et le pentan-1-ol permet d'obtenir un ester le butanoate de pentyle de formule brute C9H18O2, dont l'odeur rappelle celle de l'abricot. Le taux d'avancement final de la réaction est 0,67 à partir d'un mélange équimolaire (n0= 100 mmol) d'acide et d'alcool maintenu à la température de 50°C avec un montage à reflux.
- Quelle est la valeur de la constante d'équilibre de la réaction ?
0,25 ; 61,5 ; 0,016 ; 4 ; 0,67 ; 2.
corrigé
Qté de matière : acide benzoïque 12,2 / 122 = 0,1 mol
alcool : masse = 40*0,791 = 31,64 g ; 31,64 / 32 = 0,988 mol (en excès)
Qté de matière théorique d'ester : 0,1 mol soit 0,1*136= 13,6 g
rendement = masse expérimentale / masse théorique = 10,2 / 13,6 = 0,75 (75%)
acide + alcool = ester + eau
K= [ester]éq[eau]éq/([acide]éq[alcool]éq)
[ester]éq=[eau]éq= tc ; [acide]éq=[alcool]éq=(1-t)c
K= (tc)² / ((1-t)c)² = t² / (1-t)²= 0,67 ² / (1-0,67)² = (0,67/0,33)² = 4.
|
pile ; électrolyse
- On réalise l'électrolyse d'une solution de nitrate d'argent avec des électrodes inattaquables de graphite. On observe à l'anode l'oxydation de l'eau en dioxygène et à la cathode un dépôt d'argent. L'électrolyse dure 15 min, l'intensité du courant étant maintenue constante et égale à 0,08 A
Données : 1 Faraday = 96 500 C ; M(Ag= = 107,9 g/mol.
- Quelle est la masse (mg) du dépôt d'argent à la cathode ?
81 ; 40 ; 162 ; 20 ; 12,5 ; 10,8.
- Quelle est la quantité (mmol) du gaz formé à l'anode ?
0,75 ; 0,19 ; 1,5 ; 0,09 ; 3 ; 0,37.
- On réalise une pile cadmium argent contenant les couples oxydo-réducteur Ag+/Ag ; Cd2+/ Cd.Les solutions électrolytiques ont une concentration initiale en ion métallique égale à 0,15 mol/L. La partie immergée de l'électrode de cadmium a une masse de 3g. Lorsque la pile fonctionne, la masse de l'électrode de cadmium diminue et il se forme un dépôt d'argent sur l'électrode d'argent.
Données : Cd=112,4 ; Ag=108 g/mol.
- Quel est l'avancement de la réaction (mol) lorsque tout le cadmium immergé est consommé ?
1 ; 0,15 ; 0,5 ; 0,027 ; 0,30 ; 0,96.
- Quelle est la masse d'argent (g) formée sur la partie immergée de l'électrode d'argent ?
5,8 ; 3 ; 1,6 ; 6 ; 2,9 ; 2,1.
corrigé
Ag++ e- --> Ag à la cathode.
Qté d'électricité Q=I t = 0,08*15*60 = 72 C
Qté de matière d'électron = Qté de matière d'argent = 72/96500 = 7,46 10-4 mol.
masse d'argent : 7,46 10-4 *107,9 = 0,08 g = 80 mg.
à l'anode H2O--> ½O2 + 2H++2e-.
Qté de matière de dioxygène = 0,25 fois la qté de matière d'électrons
7,46 10-4 *0,25 = 1,86 10-4 mol = 0,186 mmol.
Cd + 2Ag+ --> Cd2+ + 2Ag
|
|
Cd |
+ 2Ag+ |
2Ag déposé |
| initial |
3/112,4 = 0,0267 mol |
n0 en excès |
0 |
| en cours |
0,0267 -x |
n0 -2x |
2x |
| fin |
0,0267 -xfin = 0
xfin =0,0267 mol
|
n0 -2xfin = n0 - 0,053 |
2xfin =0,053 mol |
l'avancement de la réaction est égal à 1 quand tout le cadmium est consomé car l'avancement maximal est égal à l'avancement final.
masse d'argent déposé = 0,053*107,9 = 5,76 g.
|
| d'après concours kiné Strasbourg 03
physique 1 h - chimie ½ h- sans calculatrice.
|
|
|
dipôles
- Soit le circuit suivant :
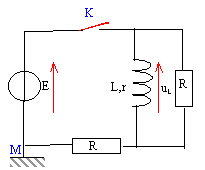
L'interrupteur K est fermé. A un instant considéré comme initial on ouvre l'interrupteur K. L= 10 mH ; R= 100 W ; E= 10 V, r =10 W.
A- Avant l'ouverture de l'interrupteur, l'intensité du courant délivré par le générateur vaut 50 mA.
B- Après ouverture de K la tension aux bornes de la bobine devient négative.
C- Après ouverture de K la tension aux bornes de la bobine tend vers zéro.
D- Après ouverture de K, l'énergie emmagasinée dans la bobine devient négative.
K fermé : en régime permanent i = E / résistance du dipôle
résistance équivalente à r et R en parallèle : R1 = rR/(r+R) = 10*100 / (10+100) = 9,09 W.
résistance équivalente à r et R1 en série : R1+R = 109,09 W.
intensité i = 10/109,1 = 91,6 mA.
uL = R1i = 9,1*0,0916 = 0,83 V
K ouvert : uL décroît de 0,83 V jusqu' à zéro. C vrai
l'énergie stockée (½Li² =0,5 *0,01 *0,0916²=4,2 10-5 J) est perdue sous forme de chaleur dans les résistances r et R. Cette énergie tend vers zéro.
- Soit un dispositif réalissant des oscillations électriques à l'aide d'uncircuit RLC. On observe la tension aux bornes du condensateur. On donne t2 = 10 ms.
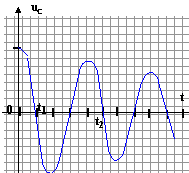
A- La tension aux bornes du dipôle ohmique est nulle en t1.
B- Le régime observé est pseudo-périodique et la pseudo-période vaut 10 ms.
C- On peut considérer que la pseudo-période vaut environ la période propre du circuit LC non amorti.
D- L'énergie stockée par le condensateur à t2 est nulle.
à t1, la tension uC est nulle : la bobine stocke toute l'énergie du dipôle et l'intensité est alors maximale. La tension aux bornes de R n'est pas nulle uR= Ri
La pseudo-période vaut environ 8 ms.
si l'amortissement est faible , la période propre du circuit LC est voisine de la pseudo-période.
à t1, la tension uC est nulle : le condensateur ne stocke pas d'énergie C et D vrais
- On réalise le circuit suivant :
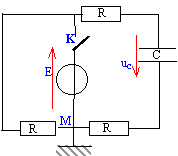
On ferme l'interrupteur. On observe alors la tension uC aux bornes du condensateur. La solution de l'équation différentielle vérifiée par uC s'écrit :
uC= E(1-exp(-t / (3RC)) ; uC= E(1-exp(-t / (2RC)) ; uC= E exp(-t / (2RC)-1) ; uC=E exp(-t / (3RC)-1) ;
K fermé : C est en série avec une résistance égale à 2R ; t = 2RC
uC= E(1-exp(-t / (2RC))
|
| ondes
- Dans un milieu dispersif la célérité d'une onde progressive périodique mécanique dépend :
A- Uniquement du milieu.
B- De la fréquence de l'onde.
C- De la période de l'onde.
D- de l'amplitude de l'onde du milieu et de la fréquence ( donc de la période) B et C vrais
- On provoque simultanément à l'instant t=0 deux perturbations transversales de même forme et de même sens aux deux extrémités d'une corde tendue de longueur 10 m. La célérité des ondes le long de cette corde est de 20 m/s. A l'instant t=0, l'amplitude de la perturbation est nulle aux extrémités de la corde.
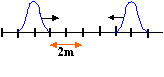
A- La corde est représentée à la date t= 0,10 s.
B- Les fronts des deux ondes se rencontrent à l'instant t= 0,2 s.
C- La durée de chaque perturbation est de 0,1 s.
D- A l'instant t= 0,3 s on observe une perturbation transversale unique.
distance parcourue par la perturbation à t = 0,1 s : d = 20*0,1 = 2 m alors que le dessin indique 3 m.
à t = 0,3 s , les deux perturbation se recouvrent exactement ( addition) C et D vrais
- Une onde sonore de fréquence 400 Hz se propage dans une tige métallique avec une célérité de 3000 m/s.
A- L'onde se propage transversalement
B- Deux points distants de 15 m sont en phase.
C- Deux points distants de 26,25 m sont en opposition de phase.
D-Deux points distants de 35 m sont en opposition de phase. deux points en phase sont distants de k l ( k entier) ; l = 3000 / 400 = 7,5 m
deux points en opposition de phase sont distants de (2k+1) ½l ( k entier) ;
26,25 / (0,5*7,5) = 7 ; 35 / (0,5*7,5) =9,3
7 est un entier impair ; 9,33 n'est pas un nombre entier B et C vrais
- On observe à l'aide d'un faisceau laser, de longueur d'onde dans le vide l0 = 600 nm une fente de largeur a = 0,1 mm et de centre O découpée dans un écran E'. On place à la distance D= 2 m et parallèlement à E' un écran E. On observe sur cet écran une tache centrale brillante de centre A, et des taches latérales brillantes, symétriques par rapport à A et de moins en moins lumineuses à mesure que l'on s'éloigne de A. Soient B et B' les centres des taches sombres qui encadrent la tache centrale.
A- Le phénomène observé est celui de la réfraction de la lumière.
B- L'angle q= angle (AOB), appelé écart angulaire vaut 0,012 rad.
C- La largeur de la tache centrale vaut 2,4 cm.
D- la position des taches sombres dépend de la longueur d'onde. phénomène de diffraction
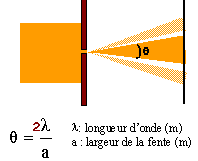
angle (AOB) = ½q = l /a = 600 10-9 / 10-4 = 6 10-3 rad ;
tan q = ½largeur tache centrale / D soit largeur = 2 D tanq = 2*2*6 10-3 =2,4 10-2 m = 2,4 cm. C vrai
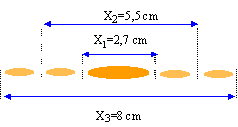
X2 = 2 X1 et X1 = 2lD/a D vrai
- L'énergie d'ionisation d'un atome d'hydrogène pris dans son état fondamental est de 13,6 eV.
A- Il est impossible d'ioniser un atome d'hydrogène en le bombardant avec des électrons de vitesse égale à 1,8 106 m/s
B- Si on se place dans l'hypothèse où l'atome est ionisé, alors l'énergie de l'électron émis est quantifiée.
C- La longueur d'onde de la radiation susceptible d'ioniser l'atome d'hydrogène à partir de son état fondamental est approximativement de 10-7 m
D- Un électron d'énergie cinétique 2 eV vient heurter un atome d'hydrogène au niveau correspondant à n=3, d'énergie E3= -1,5 eV: l'atome s'ionise.
h= 6,63 10-34 J s ; e = 1,6 10-19 C ; c= 3 108 m/s ; masse électron : 9,1 10-31 kg ; 1,8² voisin 3,2. ½mv² = 0,5*9,1 10-31*(1,8 106)² = 4,05*3,64 10-18 = 14,8 10-19J
14,8 10-19 / 1,6 10-19 = 9,2 eV, insuffisant pour ioniser l'atome car inférieur à 13,6 eV.
E = 13,6 * 1,6 10-19 = 2,2 10-18 J ;
l = hc/E = 6,6 10-34*3 108 / 2,2 10-18 = 9 10-8 m C et D vrais
|
mécanique
- Un oscillateur est constitué par une masse ponctuelle m = 0,2 kg accrochée à un ressort de raideur k = 5 N/m. La masse oscille sans frottement suivant un axe (x'Ox) horizontal sur lequel on la repère par son abscisse x. Lorsque le ressort est non allongé, x=0. A l'instant t=0 la masse est située à l'origine et est animée d'une vitesse de 60 cm/s vers les x négatifs. L'équation horaire du mouvement est donnée dans le système S.I par :
A- x= -0,12 sin(5t)
B- x= 0,6 sin( 0,2t)
C- x= 0,12 sin(5t)
D- x= - 0,6 sin(5t + ½p) w² = k/m= 5 / 0,2 =25 et w = 5 rad/s.
à t = 0 , x=0 donc fonction sinus
conservation de l'énergie mécanique du système {mase- ressort} : ½ka² = ½mv²max.
a² = m/kv²max = 0,2 / 5 *0,6² = 144 10-4 soit a = 0,12 m
le solide se dirige vers les x négatifs à t =0 A vrai
- On enregistre l'amplitude oscillatoire d'un dispositif constitué par un ressort de raideur k à l'extrémité duquel est fixé un solide de masse M. L'ensemble est soumis à un dispositif d'amortissement équivalent à une force de frottement fluide. Un oscillateur mécanique impose une fréquence oscillatoire au système masse ressort. On relève l'amplitude oscillatoire en fonction de la fréquence imposée par l'excitateur pour deux amortissements différents, l'un faible, l'autre plus fort. k= 1,8 N/m et M= 0,5 kg.
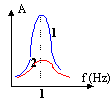
A- La courbe 1 correspond à l'amortissement le plus faible.
B- La pulsation du système ressort-masse vaut environ 6 rad/s.
C- Les deux courbes caractérisent un phénomène de résonance.
D- Seule la courbe 2 caractérise un phénomène de résonance.
fréquence de résonance f = 1 Hz ; w = 2p f = 6,28 rad/s.
courbe 2 : faible amplitude, amortissement grand, donc résonance "floue", peu marquée. A et B vrais
- Une bille d'acier de rayon r = 5 mm tombe verticalement dans l'eau. La valeur de la force de frottement fluide exercée par l'eau a pour expression F= KAreauV² où A = pr² est la surface de la section droite de la bille et K un coefficient constant qui dépend de la forme du solide. On néglige la poussée d'Archimède. reau= 1000 kg/m3 ; racier = 8000 kg/m3 ; K= 0,2 ; g = 10 m/s² ; racine carrée (8/3)=1,6 ; racine carrée (20/3)= 2,6.
A- L'équation différentielle du mouvement du centre d'inertie G de la bille est : mdv/dt + KAreauV² = mg.
B- L'équation différentielle du mouvement du centre d'inertie G de la bille est : mdv/dt - KAreauV² = mg.
C- La valeur de la vitesse limite est 2,6 m/s.
D- La valeur de la vitesse limite est 1,6 m/s. poids, vertical vers le bas , valeur mg ;
frottement, vertical vers le haut, valeur : KAreauV²
la seconde loi de Newton s'écrit, en projection sur un axe vertical vers le bas : mg-KAreauV² = ma = mdv/dt
mdv/dt + KAreauV² = mg
vitesse limite v²lim = mg / (KAreau)
volume de la bille : 4/3 p r3 ; masse de la bille : 4/3 p r3 racier ; K= p r²
v²lim =4rg racier / (3Kreau) = 4*5 10-3 *10*8000/(0,2*3*1000)= 8/3 ; vlim = 1,6 m/s.
A et D vrais
- Un satellite de masse m, considéré comme ponctuel, est mis en orbite circulaire autour du centre de la terre. Il évolue à une altitude z par rapport à la surface de la terre. La terre est de rayon R et de masse M.
A- Le satellite subit une force d'attraction de valeur : F=GM/(R+z)²
B- L'accélération du satellite est centrifuge.
C- La période de révolution du satellite est T= 2p(R+z)3/2 / (GM)½. F= MGm / (R+z)² ; a = GM/(R+z)² = v²/(R+z)centripète
v² = GM/(R+z);
période T : durée pour décrire une circonférence de rayon R+z à la vitesse v
2p(R+z) = vT soit 4p²(R+z)² = v²T² = GM T²/(R+z);
T² = 4p²(R+z)3 / (GM). C vrai
- On considère le mouvement du centre d'inertie G d'un solide en chute libre lancé verticalement à partir du sol, dans un champ de pesanteur uniforme avec une vitesse v0 non nulle.
A- La trajectoire de G est toujours une parabole.
B- Au sommet de la trajectoire , vG est nulle.
C- La valeur vG de la vitesse de G dépend de l'altitude du projectile et de sa vitesse initiale.
D- L'altitude du sommet ne dépend que de la valeur v0 de la vitesse initiale. lancé vertical : trajectoire rectiligne
au sommet de la trajectoire verticale, la vitesse est nulle
conservation de l'énergie mécanique du solide : au départ : ½mv²; au sommet : mgh ; v² = 2gh
h : différence d'altitude entre le départ et le sommet ;
h dépend de la vitesse initiale et de g. B et C vrais
- A l'intérieur d'un aérostat, l'air contenu dans une enveloppe est remplacé par du dihydrogène. On suppose que la masse de l'enveloppe est de m = 88 kg. La masse de la nacelle est notée M. l'enveloppe contenant le gaz a un volume V= 400 m3. L'air environnant a une masse volumique rair = 1,2 kg/m3 et H2 a une masse volumique rH2 = 0,08 kg/m3. g = 10 m/s².
A- La valeur de la poussée d'Archimède est de 4800 N.
B- La valeur de la poussée d'Archimède est de 320 N.
C- La valeur maximale de M pour que l'aréostat décolle est de 392 kg.
D- La valeur maximale de M pour que l'aréostat décolle est de 360 kg. poussée d'Archimède due à l'air extérieur : Vrair = 400*1,2*10 = 4800 N
poids de la nacelle, de l'enveloppe et du dihydrogène ( enveloppe fermée) : g(M+88 + 0,08*400 )= (120+M)g
si 4800 >(120+M)g alors on décolle ; M<360 kg
A et D vrais
- On a représenté la vitesse v en fonction du temps pour un mobile se déplaçant sur un plan horizontal.
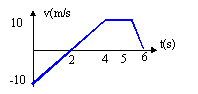
A- Le mouvement du mobile est uniforme durant les 4 premières secondes.
B- la valeur de l'accélération du centre d'inertie du mobile à t = 5s = est de 10 m/s².
C- Le mouvement du mobile ne peut qu' être rectiligne durant les 4 premières secondes.
D- Le mouvement du mobile change de sens à t = 5s.
0<=t<2s : la valeur de la vitesse décroît de 10 à 0 m/s a = (0-10)/2 = -5 m/s²
à t = 2s, arrêt puis changement de sens.
2<t<=4s , la valeur de la vitesse croît de 0 à 10 m/s ; a = 10/2 = 10 m/s²
4<t<=5, la valeur de la vitesse est constante, mouvement uniforme.
5<t<=6, la valeur de la vitesse décroît de 10 à 0 ; a = -10 m/s². C vrai
- Un skieur de masse m=90 kg s'élance à partir d'une position de repos sur une piste rectiligne, inclinée d'un angle a = 30° par rapport à l'horizontale. La valeur F des forces de frottements varie avec la vitesse selon la loi F= kv² avec k=0,5.
A- k est en kg m-1.
B- L'équation différentielle du mouvement du centre d'inertie de G du skieur est : mg sin 30 - kv² = m dv/dt.
C- L'équation différentielle du mouvement du centre d'inertie de G du skieur est : mg cos 30 - kv² = m dv/dt.
D- La vitesse limite que peut atteindre le skieur au bout d'un temps très long est 30 m/s. F=kv² soit k = F/v²; force = masse * accélération : kg m s-2 ; vitesse ² : m² s-2.
k : kg m s-2 m-2 s² soit kg m-1.
poids du skieur, vertical vers le bas, valeur mg
frottement parallèle au plan, sens contraire à la vitesse, valeur F=kv²
action normale du plan, perpendiculaire au plan, valeur N=mg cos30
la seconde loi de Newton s'écrit sur un axe parallèle au plan dirigé vers le bas :
mg sin 30 -kv² = ma = mdv/dt
vitesse limite v²lim =mg sin 30 /k = 90*10*0,5 / 0,5 = 900 ; vlim = 30 m/s. A, B et D vrais
|
|
|
radioactivité
- Un laboratoire étudie un échantillon de césium 137 de date de fabrication et de masse inconnues. Le graphe représente l'évolution de la masse de césium 137 en fonction du temps. La demi-vie du césium 137 est : 1957 ans ; 1965 an ; 35 ans ; 30 ans.
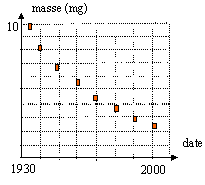
à t½ la masse initiale de 137Cs est divisée par deux: lecture graphe t½= 35 ans.
- On considère une substance radioactive qui émet 2 107 particules alpha par seconde et dont la demi-vie est 10 s. Le nombre de noyaux radioactifs dans cette substance est : 2 108 ; 1,4 106 ; 1,4 107 ; 2,9 108. A = 2 107 Bq; A= lN avec l = ln2 / t½ = 0,7 / 10 = 0,07 s-1.
N= A/l =2 107 / 0,07 = 2/7 109 = 2,9 108 noyaux.
- Données : plomb 82Pb; uranium 92U.
L'uranium 238 subit plusieurs désintégrations successives de type a et b - et se transforme en plomb 206. Le nombre de désintégrations de chaque type pour passer de l'uranium 238 au plomb 206 est :
A- 8 désintégrations de type a et 6 désintégrations de type b -.
B- 6 désintégrations de type a et 8 désintégrations de type b -.
C- 8 désintégrations de type a et 1 désintégrations de type b -.
D- 4 désintégrations de type a et 3 désintégrations de type b -. 23892U--> 93AX + -10e Z augmente de1 et A est constant
23892U--> 91234Y + 24He Z diminue de 2 et A diminue de 4.
or 238-206 = 32 donc 8 désintégrations a.
8 désintégrations a entraînent une diminutions de 16 pour Z
or Z diminue seulement de 92-82 = 10 ; donc 6 désintégrations b -. A vrai
- Le diagramme énergétique de l'atome de sodium est donné.
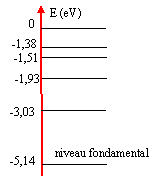
On considère un atome de sodium non excité. h= 6,62 10-34 Js ; c= 3 108 m/s ; e = 1,6 10-19 C; raie jaune du sodium l= 589 nm ; Les photons visibles ont des énergies comprises entre 1,6 et 3,1 eV.
A- l'énergie d'ionisation de l'atome de sodium vaut 8 10-19 J.
B- La transition entre les niveaux -1,93 eV et -5,14 eV correspond à une radiation UV.
C- Lorsque l'atome de sodium absorbe de l'énergie, son énergie diminue.
D- La transition entre les niveaux - 1,93 et -1,51 eV correspond à une radiation du système visible.
5,14*1,6 10-19 = 8,2 10-19 J
E= 5,14-1,93 = 3,21 eV; 3,21*1,6 10-19 = 5,14 10-19 J
l = hc/E =6,6 10-34 *3 108 / 5,14 10-19 = 3,85 10-7 m = 385 nm (U.V)
E= 1,98-1,51 = 0,42 eV valeur située hors de l'intervalle [1,6 ; 3,1 eV] des énergies des photons du domaine visible. A et B vrais
- Le spectre d'émission de l'atome d'hydrogène présente plusieurs raies d'émission dans le visible. Les longueurs d'onde exprimées en nm corespondant aux transitions sont : 656 nm ; 486 nm ; 434 nm ; 410 nm. le niveau fondamental est situé à -13,6 eV.
A- L'énergie de l'atome d'hydrogène est quantifiée.
B- La raies à 656 nm est celle des photons émis de plus faible énergie.
C- Si l'énergie apportée à l'atome d'hydrogène est supérieure à 13,6 eV, l'atome est ionisé.
D- La lumière émise par l'hydrogène est rouge.
l = hc/DE ; l est d'autant plus grand que DE est plus petit.
la lumière émise correspond à un spectre de raies d'émission 656 nm ( jaune) ; 486 nm 434 nm et 410 nm (vet bleu violet)
A, B et C vrais
|
chimie
- On dose 100 mL d'une solution d'hydroxyde de sodium (placée dans un bécher ) par une solution d'acide chlorhydrique ( placée dans la burette). On place un conductimètre dans le bécher et on mesure la conductance G au cours du dosage. On néglige l'effet de dilution.l(H3O+)= 35 10-3 S.I ; l(HO-)= 20 10-3 S.I ; l(Na+)= 5 10-3 S.I ; l(Cl-)= 8 10-3 S.I ;
A- On obtient la courbe suivante qui représente l'évolution de G en fonction du volume de solution d'acide chlorhydrique versé. 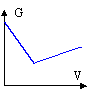
B-Après l'équivalence, l'avancement de la réaction de dosage ne cesse d'augmenter
C- A l'équivalence on obtient une solution de chlorure de sodium
D- Après l'équivalence le réactif titré devient le réactif limitant.
Na+ et HO- dans le bécher ; ajout H+ et Cl- ; H+ + HO- --> H2O
avant l'équivalence : cela revient à remplacer HO- par Cl- ; or l(Cl-)<l(HO-) donc la conductivité s diminue dans le bécher
après l'équivalence on ajoute H+ par Cl- donc s augmente
de plus s et la conductance G sont proportionnelles.
A, C et D vrais
- L'ion fer II peut être oxydé par l'ion permanganate en milieu acide. On utilise cette réaction pour doser une solution contenant des ions fer II. Couples redox : MnO4- / Mn2+ ; Fe3+ / Fe2+.
A- L'équation bilan de la réaction de dosage est : MnO4-+ 5 Fe2++ 8H+--> Mn2+ +5 Fe3++4H2O
B- On a à l'équivalence la relation n(MnO4-)versé = 5 n( Fe2+) dosé.
C-Avant l'équivalenc, le bécher contenant les ions fer II est de couleur rose violacée.
D- A l'équivalence, la quantité de matière initiale du réactif titré est égale à la quantité de matière introduite du réactif titrant. 5 fois{ Fe2+ = Fe3+ + e-} oxydation
MnO4- + 8H+ + 5 e- = Mn2+ + 4H2O réduction
MnO4-+ 5 Fe2++ 8H+--> Mn2+ +5 Fe3++4H2O
|
|
MnO4- ajouté |
+ 5 Fe2+. |
| initial |
0 |
nFe2+ |
| en cours |
x |
n( Fe2+) -5x |
| équivalence |
n(MnO4-) = xéqui |
n( Fe2+) -5xéqui = 0 |
xéqui = n(MnO4-) = n( Fe2+) /5.
avant l'équivalence la solution dans le bécher est incolore ( Fe2+ en excès) ; après l'équivalence la solution est violette (MnO4- en excès. A vrai
- On dispose d'une solution aqueuse de chlorure de fer III. On mesure la conductance de cette solution à l'aide d'une cellule conductimétrique, constituée de 2 électrodes parallèles de surface S, distantes de L.
A- La conductivité de la solution est donnée par la relation : s = l(Cl-)[Cl-]+3l(Fe3+)[Fe3+].
B- La conductance est donnée par G= s S/L.
C- La conductivité dépend de la température de la solution.
D- En changeant de conductimètre, on obtient la même valeur de la conductance qu'avec le premier. s = l(Cl-)[Cl-]+l(Fe3+)[Fe3+] avec 3 [Fe3+] = [Cl-]
G (S) = s (S m-1) S ( m²) / L (m)
en changeant de cellule de mesure on modifie S/L, donc G. B et C vrais
- La conductivité d'une solution saturée d'hydroxyde de zinc (Zn2+ + 2HO-) vaut s =2 10-4 Sm-1. l(Zn2+) = 10 10-3 S.I ; l(HO-)= 20 10-3 S.I ;
A- La conductivité molaire ionique est donnée en Sm² mol-1.
B- La solubilité de l'hydroxyde de zinc est donnée par la relation : s = s / (2l(Zn2+)+l(HO-))
C- La solubilité de l'hydroxyde de zinc est s = 4 10-3 mol /L.
D- La solubilité de l'hydroxyde de zinc est s = 5 10-3 mol /L. s = l(Zn2+)[Zn2+] +l(HO-)[HO-] avec s =[Zn2+] et 2 [Zn2+] = [HO-]
s = [l(Zn2+) +2l(HO-)]s soit s = s /[l(Zn2+) +2l(HO-)]= 2 10-4 / (10+2*20)10-3]= 4 10-3 mol m-3.
A vrai
- Expérience 1 : on ajoute de la poudre d'argent en excès à une solution de nitrate de fer (III) de concentration c= 0,01 mol/L. On agite le système jusqu'à ce que l'équilibre soit atteint. Les concentrations des espèces dissoutes valent alors : [Fe3+]éq=3,3 10-4 mol/L ; [Fe2+]éq=[Ag+]éq=0,01 mol/L.
Expérience 2 : on introduit dans un bécher une solution de nitrate de fer (III), une solution de nitrate de fer (II°, une solution de nitrate d'argent et un peu de poudre d'argent. Le volume final de la solution est égal à 1 L. On donne les concentrations initiales des espèces chimiques dans le mélange [Fe3+]i=4 10-5 mol/L ; [Fe2+]i=0,012 mol/L et [Ag+]i=3 10-3 mol/L
A- L'expérience 1 permet de calculer la constante d'équilibre K de la réaction. sa valeur est 0,3.
B- L'expérience 1 permet de conclure que le quotient initial de la réaction est nul.
C-Dans l'expérience 2, la masse d'argent solide va augmenter.
D- Dans l'expérience 2, la masse d'argent solide va diminuer. Fe3+ + Ag = Fe2+ + Ag+. K = [Fe2+]éq[Ag+]éq/[Fe3+]éq= 0,01² / 3,3 10-4 = 0,3.
expérience 1 : Qr,i = [Fe2+]i[Ag+]i/[Fe3+]i= 0 ;
expérience 2 : Qr,i =0,012*3 10-3 / 4 10-5 = 1,2*3/4 = 0,9 valeur supérieure à K , donc délacement dans le sens indirect : formation Ag.
A, B, C vrais
- La charge d'une mole d'électrons est 96500 C. On considère une pile alcaline dont l'équation de la réaction de fonctionnement global est : Zn(s) + 2MnO2(s)+H2O--> ZnO(s) + 2MnO2H(s).
On appelle capacité en charge la valeur Qmax de la quantité d'électricité débitée par la pile. Elle vaut 48250C.
A- La quantité d'électrons débités par la pile est de 2.
B- La quantité d'électrons débités par la pile est de 0,5.
C- La quantité de zinc consommé est 0,25 mol.
D- La quantité de zinc consommé est 1 mol.Ag. n e- = 48250 / 96500 = 0,2 mol d'électrons
Zn + 2HO- = ZnO + H2O + e- d'où nZn = ½ n e- = 0,25 mol. B, C vrais
- A- Dans un électrolyseur, le courant entre par l'anode.
B- Dans un électrolyseur, le courant entre par la cathode.
C- Lors de la décharge, un accumulateur joue le rôle de récepteur.
D- Lors de la décharge, un accumulateur joue le rôle de générateur. A, D vrais
- Couples oxydant / réducteur : O2/H2O ; H2O/H2 ; Pb2+ / Pb ; H+ / H2.
On effectue l'électrolyse de nitrate de plomb en utilisant des électrodes inattaquables de graphite. Les ions nitrates sont indifférents. Il se dépose du plomb à la cathode et il se forme un gaz incolore à l'anode. L'intensité du courant est constante, égale à 1,2 A. La durée du fonctionnement de l'électrolyse est de 20 min.
A- Le gaz incolore est le dioxygène.
B- Le gaz incolore est le dihydrogène.
C- La quantité de plomb déposé est d'environ 15 mmol.
D- La quantité de plomb déposé est d'environ 7 mmol. à l'anode oxydation de H2O : H2O = ½O2 + 2H+ + 2e-.
à la cathode réduction de : Pb2+ + 2e- = Pb.
Q= I t = 1,2* 20*60 = 1440 coulombs ; n e- = 1440 / 96500 = 0,015 mol soit 15 mmol
donc nPb = 7,5 mmol A, D vrais
- On dissout un acide AH faible dans l'eau pour réaliser une concentration égale à c= 0,1 mol/L. On mesure t le taux d'avancement final de la réaction de dissolution dans l'eau t = 0,01.
A- La constante d'équilibre de la réaction vaut K= 10-5.
B- Si la concentration de l'acide augmente alors t augmente.
C- La valeur du quotient de réaction dans l'état d'équilibre est indépendant de la concentration de l'acide.
D- Le pH est supérieur à 5. K = [A-]éq[H3O+]éq / [AH]éq=t² c / (1-t) = 10-4 *0,1 / (1-0,01 ) = 10-5.
K ne dépend que de la température ; à une température donnée si c croît alors t diminue.
[H3O+]éq =t c = 0,01*0,1 = 10-3 ; pH=3 A, C vrais
- L'ion éthylammonium est un acide faible dont la base conjuguée est l'éthylammine. La réaction de dissolution de cet acide dans l'eau conduit à un équilibre chimique suivant la réaction : C2H5NH3+ + H2O = C2H5NH2 + H3O+. La constante d'équilibre associée à cet équilibre vaut 2 10-11. On donne log 2 = 0,3 ; log 5 = 0,7 ; Ke = 10-14.
A- Le pka du couple ion éthylammonium / éthylammine vaut environ 11.
B- L'éthylamine réagit avec l'eau pour donner une solution basique.
C- la constante d'équilibre de la réaction de l'éthylamine avec l'eau vaut 5 10-4.
D- La réaction entre l'éthylamine et l'acide chlorhydrique ne peut pas être considérée comme totale. K = [C2H5NH2]éq[H3O+]éq / [C2H5NH3+]éq= 2 10-11 ; log Ka = log 2-11 ; -logKa = pKa = -0,3+11 = 10,7
C2H5NH2 + H2O =C2H5NH3+ + HO- ;
K1 =[HO-][C2H5NH3+] / [C2H5NH2]=[HO-] [H3O+] [C2H5NH3+] / ([C2H5NH2][H3O+])= 10-14 / 210-11 = 5 10-4. C2H5NH2+ H3O+-->C2H5NH3+ ; K2 =[C2H5NH3+] / ([C2H5NH2][H3O+])= 1/K = ½ 1011.
A, B, C vrais
- On dissout dans 500 mL d'une solution d'acide éthanoïque de concentration c1 = 0,1 mol/L et de pH=1,9, une quantité égale à 0,05 mol d'éthanoate de sodium solide. Le pka du couple acide éthanoïque / ion éthanoate vaut 4,8.
A- Le pH de la solution diminue après dissolution.
B- Les ions éthanoates réagissent avec les ions oxonium de la solution acide.
C- Le pH augmente après la dissolution.
D- Le pH reste égal à 4,8. CH3COOH initial : 0,05 mol
CH3COOH + H2O=CH3COO- + H3O+ ; K = [CH3COO-]éq[H3O+]éq / [CH3COOH]éq= 10-4,8 ;
si on ajoute 0,05 mol d'ion CH3COO-, déplacement de l'équilibre vers la gauche.
conservation de l'élément carbone : [CH3COO-] + [CH3COOH] = (0,05 +0,05) / 0,5 = 2 mol/L
solution électréquiment neutre : [CH3COO-] + [HO-] = [Na+] + [H3O+]
[HO-] négligeable en milieu acide ; [CH3COO-] voisin [Na+] + [H3O+] = 0,05 / 0,5 +[H3O+] = 0,1 + [H3O+]
0,1 >> [H3O+] d'où [CH3COO-] voisin 0,1 et [CH3COOH] voisin 0,1 mol/L d'où pH fin proche de pKa = 4,8.
B, C vrais
- On dose 400 mL d'une solution d'ammoniaque de concentration inconnue par 100 mL d'une solution d'acide chlorhydrique de concentration c= 0,1 mol/L. Ces proportions correspondent à l'équivalence. pKa (NH4+ / NH3)=9,1.
A- La réaction de dosage peut être considérée comme totale.
B- A l'équivalence 0,02 mol d'ammoniac ont réagi.
C- Après avoir versé 50 mL d'acide le pH vaut 4,5.
D- Le quotient initial de la réaction s'effectuant dans le mélange précédent est supérieur à la constante d'équilibre de cette réaction. NH3 + H3O+ --> NH4+ + H2O ; K = [NH4+]/([H3O+] [NH3])=1/ Ka = 109,1 ;
à l'équivalence : 0,1 * 0,1 = 0,01 mol d'acide versé= 0,01 mol d'ammoniac ayant réagi
|
|
NH3 |
H3O+ versé |
NH4+ |
| initial |
n= 0,01 mol |
0 |
0 |
| en cours ( x= 0,005) |
0,01 -x= 0,005 mol |
x = 0,005 mol |
0,005 mol |
| équivalence |
0 |
0,01 mol |
0,01 mol |
après avoir versé 50 mL d'acide on se trouve à la demi-équivalence et pH=pKa = 9,1
Qr,i = [NH4+]i/([H3O+]i [NH3]i) est inférieure à K car la réaction évolue dans le sens direct. A vrai
- On mélange une solution aqueuse de peroxyde d'hydrogène avec une solution aqueuse d'iodure de potassium Le peroxyde d'hydrogène du couple H2O2/H2O oxyde l'ion iodure du couple I-/I2 en diiode, en milieu acide.Le diiode en solution présente un maximum d'absorption à lmax= 350 nm. A cette longueur d'onde, le coefficient d'exctinction molaire e= 2,5 105 mol-1 L cm-1. Dans une cuve d'un spectrophotomètre, de 1 cm de large, on introduit 3 mL d'une solution d'iodure de potassium acidifié, de concentration [I-]=0,01 mol/L puis un volume V=0,5 mL d'une solution de peroxyde d'hydrogène de concentration [H2O2] = 5 10-5 mol/L. On relève les valeurs de l'absorbance A pour lmax= 350 nm et on trace la courbe des variations de [I2] en fonction du temps.
| t(min) |
0 |
1 |
3 |
5 |
8 |
10 |
15 |
20 |
30 |
| A |
0 |
0,401 |
0,945 |
1,29 |
1,52 |
1,63 |
1,72 |
1,77 |
1,78 |
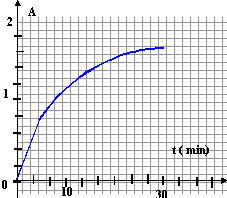
A- La quantité maximale de diiode que l'on peut obtenir est de 7,1 10-6 mol/L.
B- La quantité maximale de diiode est obtenue à la date 30 min.
C- Le temps de demi-réaction est atteint au bout de 30 min.
D- Le temps de demi-réaction est atteint au bout de 15 min.
à t = 30 min la réaction peut être considérée comme presque terminée.
H2O2 + 2I-+ 2H+ --> I2 + 2H2O
|
|
H2O2 |
+ 2I- |
I2 |
| initial |
5 10-4 * 5 10-5
= 2,5 10-8 mol
|
3 10-3 *0,01 = 3 10-5 mol |
0 |
| en cours |
2,5 10-8 -x |
3 10-5 -2x |
x |
| fin |
2,5 10-8 -xm
xm=2,5 10-8 mol
|
3 10-5 -2xm = 0
excès
|
xm=2,5 10-8 mol |
[I2]=2,5 10-8/ 3,5 10-3 = 7,1 10-6 mol/L
à t½ la moitié du réactif limitant a disparu : [I2]= 3,6 10-6 mol/L et A =e L [I2] = 2 105 *1*3,6 10-6 =0,71
soit t½ voisin de 3 min. A, B vrais
- suite du n°13.
A- La vitesse volumique de la réaction peut se mettre sous la forme v=kA avec k une constante.
B- La vitesse volumique de la réaction est proportionnelle à la dérivée de l'absorbance par rapport au temps.
C- A la date t=0, la vitesse volumique de la réaction et l'absorbance sont minimales.
D- A la date t = 30 min, la vitesse volumique de la réaction est quasiment nulle. v = 1/V dx/dt = d[I2] /dt avec [I2] =A/(e L) soit v = 1/(e L) dA/dt
à t = 0, le coefficient directeur de la tangente à la courbe A=f(t) est le plus gand possible, donc la vitesse initiale est maximale
à t >30 min, la tangente à la courbe est presque horizontale, donc la vitesse est quasiment nulle B, D vrais
- L'hydrolyse basique des huiles végétales :
A- permet d'obtenir du propan-1,2,3- triol.
B- libère de l'eau.
C- doit être réalisée à chaud.
D- utilise uniquement des solutions aqueuses d'hydroxyde de sodium. libére un ion carboxylate
soude ou potasse KOH A, C vrais
- Pour une transformation chimique non totale et catalysable :
A- Le catalyseur augmente le taux d'avancement final.
B- Le catalyseur augmente le temps de demi-réaction.
C- Le catalyseur modifie la constante de la réaction.
D- Le catalyseur intervient sur la réaction inverse. Le catalyseur permet d'atteindre plus rapidement l'équilibre sans changer ce dernier B, D vrais
|
1er sujet
- L'air est un mélange de gaz. Entourer les gaz dont la fraction molaire dans l'air est supérieur à 10 %.
Ar ; CO ; CO2 ; H2 ; H2O ; O2 ; NO2 ; N2
- Soit un bateau naviguant à une vitesse constante de 5 m.s-1 sans vent. Un singe est monté sur le mat, à 7 mètres au-dessus du pont. Il laisse tomber une noix de coco. Où tombe cette noix ? On négligera les frottements de l'air.
- Quelle est la vitesse de translation moyenne de la Terre sur son orbite autour du Soleil ?
- Quelle puissance électrique faut-il pour chauffer de 20°C à 60°C les 200 litres d'eau contenus dans un chauffe-eau en une durée de 5 h ? On considèrera ce chauffe-eau convenablement isolé thermiquement.
- Citez quatre formes d'énergie dites renouvelables pouvant être utilisées pour produire de l'électricité.
corrigé
O2 et N2.
au pied du mât tant que le mouvement est rectiligne et uniforme
hydroélectricité ; solaire, géothermie; éolien ; biomasse ( bois, colza..)
distance Terre Soleil D=1,5 1011 m ; période : T =365*24*3600 = 3,15 107 s
en supposant l'orbite circulaire :
2pD = v T soit v = 2pD / T = 6,28*1,5 1011 / 3,15 107 = 30 km/s.
capacité thermique massique de l'eau : c = 4180 J kg-1 K-1.
Q = mc Dq= 200/4180*(60-20)=3,34 107 J.
Puissance (W) = énergie (J) / durée (s) = 3,34 107 / (5*3600) = 1,85 kW.
|
| sujet 2 : dipôle RC, RLC
- Questions préliminaires :
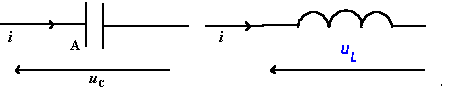
- La capacité du condensateur vaut C, l'armature A porte la charge q. Donner les relations entre : q et i, q et uC, i et uC.
- La bobine est idéale (r = 0), son inductance vaut L. Donner la relation entre i et uL.
- On considère le montage suivant :
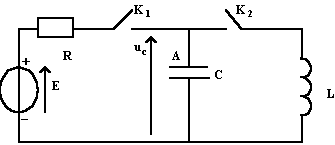
Initialement, K1 et K2 sont ouverts. Le condensateur est déchargé. R1 = 1 kW ; C= 10mF ; L=1H ; E=10 V
- On ferme l'interrupteur K1 à t = 0 et K2 reste ouvert, le condensateur se charge à travers R. Donner l'équation différentielle vérifiée par uC(t).
- Quelle est l'expression littérale de la constante de temps t ?
- Donner la solution littérale de l'équation différentielle précédente.
- A l'instant t1=10 ms on ouvre K1 et on ferme K2 de façon simultanée.On note q la charge portée par l'armature A.
- Donner la valeur numérique, notée U0 de uC(t) à l'instant t1.
- A partir de l'instant t1, donner l'équation différentielle vérifiée par q (t), puis la nouvelle équation différentielle vérifiée par uC(t).
- Quelle est la valeur numérique de la période T0 des oscillations.
- De façon très schématique, esquisser l'allure de la tension uC(t) depuis l'instant t0. corrigé
i = dq/dt = q' ( dérivée de la charge par rapport au temps)
Q=CuC soit i = CduC /dt = Cu'C ; uL=Ldi/dt = L i'
- E= Ri + uC ; E=RCu'C + uC ; u'C + 1/(RC) uC = E/(RC)
constante de temps t = RC= 103*10-5 = 0,01 s = 10 ms.
solution de cette équation différentielle : uC = E(1-e-t/t)
U0 = E(1-e-1) = 0,63 E = 6,3 V.
décharge du condensateur à travrs la bobine : uC = L di/dt avec i = -dq/dt = -CduC /dt = -Cu'C ; i' = -Cu"C ;
uC = L(-Cu"C ) soit u"C + 1/(LC)uC =0
w0² = 1/(LC) = 1/(10-5) = 105 soit w0= 316,2 rad/s.
T0 = 2p/w0= 2*3,14 / 316,2 = 0,02 s = 20 ms.
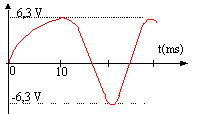
|
| Détermination de l'âge d'une momie
En effectuant des fouilles, on a découvert une momie. Pour déterminer la date approximative de sa mort, on utilise la méthode de datation au carbone 14. Cet isotope du carbone est constamment produit lors du bombardement de l'azote atmosphérique par les neutrons cosmiques. Le carbone 14, assimilé par les organismes vivants, se trouve donc présent en très faible quantité dans ces organismes. L'expérience montre que la proportion R des deux isotopes et est la même dans l'atmosphère et dans les organismes vivants : 1 atome de 14C pour 106 atomes de 12C. Après la mort, la proportion de 14C diminue car il est radioactif b-, de demi vie t½ = 5570 ans.
- Ecrire l'équation de désintégration du 14C et donner le nom des produits de la réaction.
- Dans un prélèvement de m = 100 mg de matières organiques sur la momie, on constate qu'il y a r=10% en masse de carbone. Cet échantillon présente une activité de 1 180 Bq. Calculer la constante radioactive l.
- Evaluer le nombre N0 d'atomes de 14C contenus dans l'échantillon lors de l'ensevelissement (la masse de 14C est négligeable devant la masse totale de carbone).
- Quelle était l'activité A0 de l'échantillon au moment de la mort.
- En déduire l'âge approximatif t de la momie.
masse molaire : C = 12 g/mol. constante d'Avogadro : NA=6 1023.
deuxième ligne du tableau périodique : Li, Be, B, C, N, F, Ne.
corrigé
146C --> AZX + -10e
conservation du nombre de nucléons : A+0 = 14
conservation de la charge : 6=Z-1 soit Z= 7 ( élément azote N)
l= ln2 / t½ =0,693 / 5570 = 1,244 10-4 an-1 ou 0,693 / (5570*365*24*3600) = 3,94 10-12 s-1.
masse de carbone 0,01 g ; 0,01 / 12 = 8,333 10-4 mol de carbone
nombre de noyaux : 8,333 10-4 * 6 1023 = 5 1020 noyaux
N0 = 5 1020 / 106 = 5 1014 noyaux 14C au moment de l'ensevelissement
activité A0 = lN0 =3,94 10-12 *5 1014 =1970 Bq.
A = A0 e-lt ; ln (A0/A) =l t soit t =1/l ln (A0/A) = 1/1,244 10-4 * ln(1790/1180)= 3350 ans.
|
|
|
sujet 4
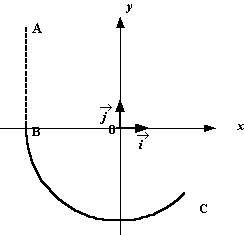
A(-R ; h) ; B(-R ; 0) ; C(0,7 R ; -0,7 R)
Un point matériel M de masse m, soumis au champ uniforme de la pesanteur est lâché sans vitesse initiale en A. De B à C, il se déplace sans frottement sur un arc de cercle de rayon R et de centre O . La trajectoire reste dans le plan du cercle (O, x, y). Au-delà du point C, il est à nouveau uniquement soumis à son propre poids. On exprimera les résultats littéraux en fonction de g, R et h .
- Déterminer la vitesse absolue vB du point M en B.
- Déterminer la norme vC, puis la vitesse absolue du point M en C.
- Déterminer les coordonnées x et y du point M au-delà de C en fonction du temps. (On prendra comme origine des temps l'instant où le point M est en C).
- En déduire l'équation cartésienne de cette trajectoire.
- Déterminer la cote y maximale de cette trajectoire (en utilisant de préférence, le théorème de l'énergie).
corrigé
théorème de l'énergie cinétique ( seul le poids travaille)
entre A et B : v²B = 2gh
entre A et C : ½mv²C-0 = mg( zA-zC) = mg(h-(-0,7 R)) = mg(h+0,7R) ; v²C=2g(h+0,7 R).
le vecteur vitesse est tangent à l'arc de cercle en C.
ce qui est écrit en gras et en bleu est un vecteur.
à l'instant initial : vC(0,7 vC ; 0,7 vC) ; OM0 ( 0,7 R ; -0,7 R)
chute libre a(0; -g)
la vitesse est une primitive de l'accélération : v(0,7 vC ;-gt+ 0,7 vC)
le vecteur position est une primitive du vecteur vitesse :
OM( x= 0,7 vC t +0,7R ; y = -½gt² + 0,7 vCt -0,7 R)
trajectoire : t = (x-0,7 R) / (0,7vC)
report dans y(t) : y = -½g (x-0,7 R)²/ (0,7vC)² + (x-0,7 R)-0,7 R.
altitude maxi ym : le vecteur vitesse est horizontal et sa composante verticale est nulle soit v = 0,7 vC ;
théorème de l'énergie cinétique entre A et altitude maxi: seul le poids travaille
½m( 0,7 vC)²-0 =mg(h-ym) ; vC² = g(h-ym)
or v²C=2g(h+0,7 R) d'où : g(h+0,7 R)/2 = g(h-ym) ;
(h+0,7 R)/2 = h-ym soit ym = ½(h -0,7R).
|
sujet 5
- On effectue dans un réacteur maintenu à une température constante le mélange d'une mole d'acide acétique (ou acide éthanoïque) et d'une mole d'éthanol à la date t = 0. La réaction chimique qui s'ensuit, athermique, produit de l'eau et un produit organique X :
- De quel type de réaction s'agit-il ?
- Ecrire l'équation-bilan de la réaction.
- Donner le nom du produit X ; calculer sa masse molaire.
- Afin de suivre l'évolution chimique du système, on prélève au cours du temps des échantillons correspondant à 1/100ème en volume du mélange réactionnel, que l'on refroidit instantanément. L'acide acétique contenu dans chaque échantillon est alors dosé par une solution décimolaire (0,1 mol. L-1) de soude (hydroxyde de sodium). Le graphe suivant rend compte de l'évolution du système à partir des résultats expérimentaux.
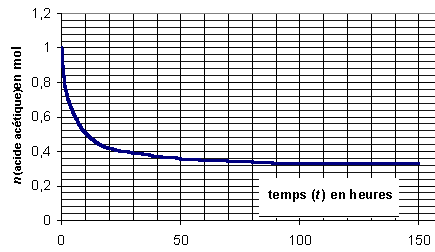
- Quel est le volume équivalent de soude versé lors du dosage de l'acide de l'échantillon à t = 50 h ?
- A partir de la courbe expérimentale donnant la quantité d'acide acétique du mélange réactionnel en fonction du temps, évaluer la vitesse instantanée de la réaction à la date t = 40 h.
- Déterminer le temps de demi-réaction.
- Calculer le rendement de la réaction à l'équilibre.
- Pour augmenter le rendement, on peut :
Réaliser au départ un mélange non équimolaire ; Augmenter la température ; Distiller le produit X formé au cours de la réaction ; Ajouter un catalyseur ; Ajouter de l'eau ; Augmenter l'agitation du mélange.
- Sur le graphique du document réponse, représenter l'allure de la courbe nacide acétique = f (t) si on réalise l'expérience en présence d'une faible quantité d'acide sulfurique.
corrigé
esterification: CH3-COOH + CH3-CH2OH=CH3-COO-CH2-CH3 + H2O
nom de l'ester : éthanoate d'éthyle ; masse molaire 88 g/mol.
à t = 50 heures, n AH= 0,36 mol soit 3,6 10-3 mol dans l'échantillon
à l'équivalence du dosage : n AH= Qté de matière de soude versée
3,6 10-3 = 0,1 v soit v = 3,6 10-2 L = 36 mL.
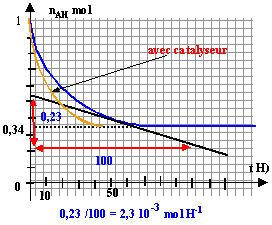
temps de demi-réaction t½ : temps au bout duquel l'avancement est égal à la moitié de l'avancement final
xfin =0,66 mol d'ester ; à t½ x = 0,33 mol d'ester soit nAH=0,67 mol. (lecture graphe t½ = 10 h)
rendement = Qté de matière d'ester obtenue / Qté de matière d'ester théoriquement possible = 0,66 / 1 = 0,66 ou 66%.
Pour augmenter le rendement, on peut :
-Réaliser au départ un mélange non équimolaire ;
- Distiller l'ester formé au cours de la réaction ;
|
| sujet 6.
On réalise un pendule simple non amorti avec une masse M (M = 500 g) accrochée à un fil de masse négligeable et de longueur L. La longueur du fil varie avec la température selon la loi L = L0(1+kq), q étant la température en degré Celcius, L0 la longueur à 0 °C et k le coefficient de dilatation k = 2.10-5 °C-1. On écarte le pendule de la position d'équilibre d'un angle a = 8 ° puis on lâche la masse sans vitesse initiale en un lieu où l'intensité de la pesanteur est g = 9,81 m/s². La période des petites oscillations de ce pendule simple est T = 2,0000 s lorsqu'il est conservé dans une enceinte à 20 °C.
- Calculer la longueur du fil L à 20 °C.
- Déterminer la vitesse v0 de la masse quand elle passe par sa position d'équilibre (a = 0 °).
- La température de l'enceinte est à présent de 0 ° C. Quelle est la période T0 du pendule précédent ?
- Une oscillation correspondant à une demi-période, combien d'oscillations effectuera-t-il en une journée (24 heures) ?
- La température de l'enceinte est à présent de q' ° C. On note que la durée de 100 périodes T est de 200,0200 s. Calculer la température q' . corrigé
période T = 2p(L/g)½ soit L = T² g / (4p²) = 9,81 / 3,14² = 0,99396 m (0,994 m)
conservation de l'énergie mécanique du système {pendule -Terre}: ½mv²0 = mgL(1-cosa)
v²0 = 2gL(1-cosa) = 2*9,81*0,994(1-cos8) = 0,19 ; v0 = 0,436 m/s.
période T0 = 2p(L0/g)½ avec L = L0(1+kq) soit L0 = L/(1+kq) = 0,994 /(1+2 10-5*20 ) =0,9936 m
T0 = 6,28(0,9936 / 9,81)½ = 1,9996 s.
nombre d'oscillations : 24*3600 / 0,9998 = 86415.
2,0002 = 2p(L/g)½ soit L =2,0002²*g / (4p²) = 0,9942 m
L = L0(1+kq') soit kq' = L/L0-1 = 0,9942 / 0,9936 -1 = 6,03 10-4.
q' =6,03 10-4/ 2 10-5 = 30°C.
|
| sujet 7
On utilise le montage ci-dessous comportant une résistance R et un condensateur déchargé C.
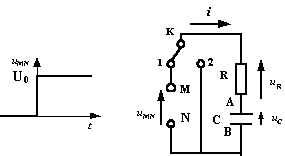
L'inverseur K étant en position 1, on applique entre les bornes M et N l'échelon de tension uMN dont l'évolution est représentée en fonction du temps t. Données : R = 2,7 kW ; C= 2,2 mF ; U0 = 12 V
- Choisir parmi les 5 courbes ci-dessous, celle qui représente l'évolution en fonction du temps t :
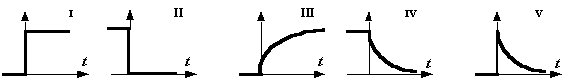
- de la tension uC aux bornes du condensateur ;
- de la tension uR aux bornes de la résistance ;
- du courant i dans le circuit.
- Donner l'expression littérale et la valeur numérique de la constante de temps t de ce circuit.
- Déterminer en régime permanent la valeur limite :
- qA de la charge de l'armature A du condensateur ;
- qB de la charge de l'armature B du condensateur ;
- EC de l'énergie emmagasinée par le condensateur.
- L'inverseur K est maintenant amené en position 2. Donner alors l'équation différentielle à laquelle obéit la tension uC aux bornes du condensateur.
- Donner, en fonction de R, C et U0, l'expression et la valeur du coefficient directeur de la tangente à l'origine de cette courbe.
corrigé
A l'instant initial ( fermeture de K) le condensateur n'est pas chargé uC=0 ; uC va ensuite croître donc courbe III
la tension uR aux bornes du résistor vaut : uMN-uC ; sa valeur initiale est uMN puis uR décroît jusqu'à s'annuler ; courbe V.
Aux bornes d'un résistor intensité et tension sont proportionnelles donc l'intensité correspond à la courbe V.
t=RC= 2700*2,2 10-6 = 5,94 ms.
qA : A relié à la borne positive du générateur lors de la charge, donc qA positive et qB= -qA négative
qA = CU0 = 2,2 10-6*12 = 2,64 10-5 coulomb.
énergie maximale stockée : ½CU²0 = 0,5 *2,2 10-6*12² = 1,584 10-4 J.
à la décharge l'intensité change de sens : -Ri + uC=0 avec i = -dqA/dt = -CduC/dt = -Cu'C
RCu'C+ uC=0 soit u'C+ 1/(RC) uC=0
solution du type uC= U0 e-t/(RC).
en dérivant : u'C= -U0 / (RC)e-t/(RC).
le coefficient directeur de la tangente à l'origine vaut : -U0 / (RC)= -12/( 5,94 10-3)= -2020 Vs-1.
|
| sujet 8
Un émetteur émet des ultrasons par salves. Deux récepteurs, disposés à deux endroits différents sur le trajet des ondes ultrasonores, permettent d'enregistrer les ultrasons émis et de les visualiser sur l'écran d'un oscilloscope. Le dispositif expérimental est schématisé ci-dessous.
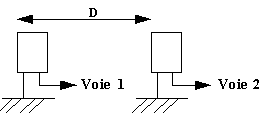
On observe à l'oscilloscope les signaux reproduits ci-dessous, la vitesse de balayage étant de 100 ms/div
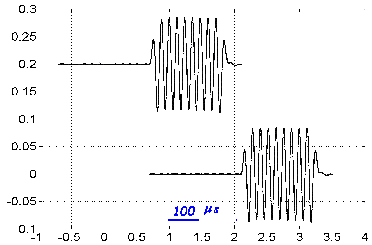
- Exprimer la longueur d'onde l en fonction de la fréquence f et de la célérité c.
- Justifier cette relation par une équation aux dimensions.
- En utilisant l'un ou l'autre des signaux, déterminer la fréquence des ultrasons.
- En comparant les deux signaux captés par les deux récepteurs distant de D = 96 mm, calculer la célérité des ultrasons dans l'air.
- Cette onde véhicule-t-elle (plusieurs réponses sont possibles) ? une information ; de la matière ; de l'énergie.
- Une onde lumineuse véhicule t-elle (plusieurs réponses sont possibles) ? une information ; de la matière ; de l'énergie.
- Donner la valeur numérique correspondant à la fréquence basse des ultrasons.
- Préciser le sens d'évolution des grandeurs suivantes lorsque l'expérience est réalisée dans l'eau. fréquence ; longueur d'onde ; célérité.
corrigé
l = c / f
f : fréquence (Hz ou s-1) ; c : célérité (m s-1 ) ; l longueur d'onde (m)
lecture graphe : 4 périodes sont représentées par 100 ms ; T= 25 m s = 2,5 10-5 s.
f = 1/ 2,5 10-5 = 40 000 Hz = 40 kHz.
retard du second signal sur le premier (lecture graphe) : 280 m s = 2,8 10-4 s
célérité : 96 10-3 / 2,8 10-4 =343 m/s.
Une onde véhicule une information, de l'énergie.
fréquence basse des ultra-sons : 20 kHz
dans l'eau : fréquence constante, caractèristique d'une onde.
la célérité est plus grande que dans l'air ; donc la longueur d'onde sera plus grande.
|
texte : Un flash électronique d'appareil photo est alimenté par deux piles de 1,5 V. Un oscillateur basse tension transforme le courant continu en courant alternatif . Un petit transformateur dont le bobinage primaire constitue l'inductance de ce circuit oscillant élève la tension qui ensuite est redressée au moyen d'une diode. Cette tension redressée permet de charger un condensateur de capacité C= 150 mF (+ ou - 10%) à une tension U=33 V.
- Etude du flash :
a- Donner l'expression de l'énergie électrique Ee stockée dans le condensateur de ce flash lorsqu'il est chargé. calculer sa valeur numérique.
b- La décharge rapide dans la lampe à éclats provoque un éclair d'une durée d'environ une milliseconde. Quelle est la valeur numérique de la puissance électrique Pe consommée par cet éclair ?
c- Pour quelle raison doit-on élever la tension avant de l'appliquer, une fois redressée, aux bornes du condensateur ?
- Etude expérimentale du circuit RC : Pour vérifier la valeur de la capacité C de ce condensateur, un élève a réalisé le montage suivant. La résistance R a une grande valeur et le générateur de tension continue a pour force électromotrice E = 12 V. A ladate t = 0, il ferme le circuit et note les intensités dans le circuit toutes les 10 secondes.
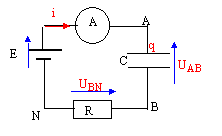
| t(s) |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
| i(mA) |
54 |
40,6 |
30,6 |
23 |
17,4 |
13,1 |
9,8 |
7,3 |
5,6 |
4,2 |
a- Sachant que le condensateur est déchargé à t=0, déterminer la valeur de la résistance R.
b- Tracer la courbe i=f(t) à partir du tableau de mesures.
c- L'intensité du courant électrique décroît en fonction du temps selon i(t) = I0e-t/t. t étant la constante de temps de ce circuit de ce circuit et I0 l'intensité à t = 0 : I0 = i(0). Quelle est la valeur numérique de l'intensité i(t ) dans ce circuit lorsque t =t ? Lire sur le graphe la valeur de t et en déduire la valeur de la capacité C de ce condensateur. Ce résultat vous semble t'il conforme aux indications du fabricant ?
corrigé
énergie électrique Ee = ½CU²
Ee = ½ *150 10-6 * 332= 8,17 10-2 J.
puissance électrique (W) = énergie (J) / durée (s) = 8,17 10-2 / 10-3 = 81,7 W.
si on n'élève pas la tension , le condensateur ne stocke pas suffisamment d'énergie et la puissance disponible est alors insuffisante pour provoquer un éclair.
Ee = ½ *150 10-6 * 32= 6,75 10-4 J ; Pe = 0,675 W.
à t=0 , uC= 0 et uR= E=RI0 soit R = 12 / 54 10-6 =2,22 105 W.
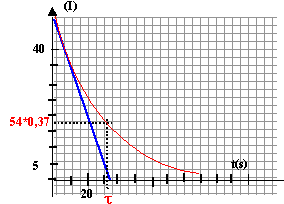
à t= t , i = 54 10-6 * e-1 = 54 10-6 * 0,37 = 1,98 10-5 A = 19,8 m A.
t voisin de 35 s ( lecture graphe) ; t = RC d'où :
C = 35 / 2,22 105 = 1,57 10-4 F = 157 m F
soit un écart de 7 sur 150 ou encore 7*100/150 = 4,7% ( résultat conforme)
|
Dans un bécher, introduit : 50 mL d'une solution de permanganate de potassium de concentration 0,20 m/L et 50 mL d'une solution d'acide sulfurique de concentration 2,0 mol/L. Puis mettre sous agitation. Prélever 1,0 mL de propan-2-ol pur ; à la date t=0 (déclencher le chronomètre), ajouter l'alcool au contenu du bécher.
Prélever rapidement un volume V=10 mL du mélange contenu dans le bécher et l'introduire dans un petit bécher. Renouveler 8 fois cette opération pour préparer huit petits béchers. A la date t1=1 minute, ajouter rapidement au contenu de l'un des béchers environ 40 mL d'eau glacée (cela s'appelle une trempe). Titrer les ions permanganate restant par une solution de sulfate de fer (II) de concentration c'=0,50 mol/L. Relever le volume équivalent v'éq.
Recommencer les opérations précédentes aux différentes dates indiquées dans le tableau ci-dessous.
Le tableau ci-dessous regroupe les résultats des différents titrages : v'éq est le volume de solution d'ions fer (II) ajouté à l'équivalence.
| t(min) |
1 |
2 |
3 |
4 |
6 |
10 |
15 |
20 |
| v'éq(mL) |
8,6 |
7,8 |
7,4 |
6,9 |
6,3 |
5,6 |
5,2 |
5 |
- Ecrire l'équation de réaction (1) d'oxydation du propan-2-ol par les ions permanganate.
- Ecrire l'équation de la réaction (2) entre les ions de fer (II) et les ions permanganate, qui sert, de support au titrage.
- Dresser le tableau d'évaluation de la réaction (2). En déduire l'expression de n = nMnO4-(aq) , quantité d'ions permanganate restant à la date t dans les 100 mL du mélange réactionnel, en fonction de c' et v'éq . Regrouper les résultats sous forme d'un tableau.
- Dresser le tableau d'évolution de la réaction (1). En déduire une relation qui exprime l'avancement x en fonction de n = nMnO4-(aq) et n0, quantité initiale d'ions permanganate. Calculer x à chaque date. Regrouper les résultats dans un tableau.
- Tracer la représentation graphique x=f(t).
- Quel est le réactif limitant dans la réaction (1) ? Que vaut l'avancement maximal de cette réaction supposée totale ? Déterminer le temps de demi-réaction.
- Comment préparer un volume de 500 mL des solutions de permanganate de potassium et de sulfate de fer (II) ?
- Quel intérêt d'effectuer une trempe avant de faire les titrages ? Comment détecter l'équivalence ?
Données : * propan-2-ol : CH3-CHOH-CH3 Densité=d=0,8 masse molaire :M=64g/mol
* permanganate de potassium : KMnO4 masse molaire : M=158g/mol
* sulfate de fer (ll) hydraté : FeSO4 ,5H2O masse molaire M=242 g/mol.
* couples oxydant/réducteur qui intervient :
Fe 3+ (aq) / Fe 2+ (aq) ; MnO4 -(aq) / Mn2+(aq)
CH3 -CO-CH3 / CH3-CHOH-CH3
corrigé
5 fois { CH3-CHOH-CH3 -->CH3 -CO-CH3 + 2H+ + 2e- }oxydation
2 fois { MnO4 -+8H+ + 5e- -->Mn2++ 4H2O } réduction
5 CH3-CHOH-CH3 +2MnO4 -+6H+ --> 5CH3 -CO-CH3 +2Mn2++ 8H2O (1)
Fe 2+ -->Fe 3+ + e- oxydation
MnO4 -+8H+ +5 Fe 2+ -->5Fe 3+ +2Mn2++ 4H2O (2)
|
|
5 Fe 2+ ajouté |
MnO4 - |
| t=0 |
0 |
n |
| t |
c' v |
n-c'v/5 |
| équivalence |
c'véq |
0= n-c'véq/5 |
d'où n = 0,2 c'véq mmol dans 10 mL si le volume est en mL et c' en mol/L.
et dans 100 mL de solution : n= 2 c'véq = 2*0,5 véq = véq mmol.
alcool : 1mL donc 0,8 g soit 0,8 / 64 = 0,0125 mol = 12,5 mmol
MnO4 - : n0 =50 * 0,2 = 10 mmol initial
|
|
5 alcool |
2MnO4 - |
| t=0 |
12,5 mmol |
n0=10 |
| t |
12,5-5x |
n0- 2x=10-2x |
| équivalence |
12,5-5xmax |
10-2xmax |
d'oùxmax = 12,5/5 = 2,5 mmol ( alcool en défaut), réactif limitant
à la date t : n0- 2x = véq (mmol) soit x = (véq -n0) / 2 mmol.
| t(min) |
1 |
2 |
3 |
4 |
6 |
10 |
15 |
20 |
| x mmol |
0,7 |
1,1 |
1,3 |
1,55 |
1,85 |
2,2 |
2,4 |
2,5 |
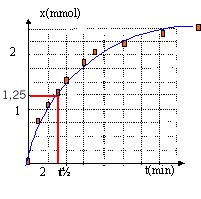
t½ voisin de 3 min, durée au bout de laquelle l'avancement est égal à la moitié de l'avancement final
préparer 500 mL de chaque solution :
0,1 mol permanganate de potassium dans 0,5 L donc peser : 158*0,1 = 15,8 g de solide puis dissoudre dans l'eau .
0,25 mol sulfate de fer dans 0,5 L donc peser 242*0,25 = 60,5 g de solide.
trempe : on réalise un blocage cinétique de la réaction (1) ce qui nous laisse le temps de doser les ions permanganate restant.
les ions permanganate jouent un double rôle : réactif et indicateur de fin de réaction :la couleur de la solution passe de du violet à l'incolore à l'équivalence. ( solution de sulfate de fer dans la burette)
|
|
|
|
réduction du diiode par le zinc :
On plonge une lame de zinc dans une solution de diiode de concentration c=0,02 mol/L et de volume V=200mL. Le zinc appartient au couple Zn2+ (aq) / Zn (s) et le diiode au couple I2 (aq) / I- (aq) .
- Ecrire l'équation de la réaction d'oxydoréduction qui se produit quand on met en présence le zinc et le diiode.
- Dans une expérience préliminaire, on étalonne un spectrophotomètre avec des solutions étalon de diiode de concentration connue. Soit A l'absorbance. Les résultats sont regroupés dans le tableau ci-dessous.
| c( mol/L) |
2 10-4 |
5 10-4 |
8 10-4 |
10 10-4 |
12 10-4 |
| A |
0,21 |
0,55 |
0,88 |
1,1 |
1,32 |
-Tracer la représentation graphique A= f ( c )
-Trouver l'équation de cette représentation graphique.
-Quelle est l'utilité de cette expérience préliminaire ?
- Pour étudier la cinétique de la réaction, on prélève 5,0 mL du mélange réactionnel que l'on place dans une fiole jaugée de 100 mL. Aux dates t indiquées dans le tableau ci-dessous, on ajoute de l'eau distillée glacée dans la fiole jusqu'au trait diluée et on la place dans le spectrophotomètre. On mesure l'absorbance A de la solution diluée.
| t(s) |
0 |
30 |
60 |
100 |
200 |
300 |
400 |
600 |
800 |
1000 |
1200 |
1400 |
| A |
1,1 |
0,88 |
0,77 |
0,67 |
0,52 |
0,42 |
0,35 |
0,24 |
0,17 |
0,12 |
0,1 |
0,08 |
- Déterminer pour chaque valeur de t, la concentration du diiode dans la solution diluée.
- En déduire la concentration du diiode dans le mélange réactionnel à chaque date t.
- Dresser le tableau d'évolution du système chimique au cours de la transformation.
- En déduire la valeur de l'avancement x à chaque date t (regrouper les résultats dans un tableau).Remarque : Le zinc est en grand excès.
- Tracer la représentation graphique x=f(t).
- Déterminer le temps de demi-réaction sachant que la transformation est totale.
- Evaluer la vitesse de réaction aux dates t=100s et t=500s. Conclure sur l'évolution de cette vitesse de réaction.
corrigé
Zn (s) + I2 (aq) à Zn2+ (aq) + 2I- (aq)
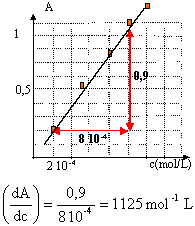
étalonage du spectrophotomètre.
c = A / 1125 mol/L ou bien A= 1125 c.
en tenant compte du facteur de dilution : 100 / 5 = 20, [I2]= 20A/1125 = 0,018 A
| t(s) |
0 |
30 |
60 |
100 |
200 |
300 |
400 |
600 |
800 |
1000 |
1200 |
1400 |
| [I2] mol/L |
20 10-3 |
16 10-3 |
13,6 10-3 |
12 10-3 |
9,2 10-3 |
7,4 10-3 |
6,2 10-3 |
4,2 10-3 |
3 10-3 |
2,2 10-3 |
1,8 10-3 |
1,4 10-3 |
Qté diiode initial : 20 10-3 *0,2 = 4 10-3 = 4 mmol
|
|
Zn |
I2 |
Zn2+ |
2I- |
| initial |
excès |
4 10-3 mol |
0 |
0 |
| en cours |
|
4 10-3 -x |
x |
2x |
| fin |
|
4 10-3 -xmax=0 |
4 mmol |
8 mmol |
xmax= 4 10-3 mol = 4 mmol
4 10-3 -x = nI2 avec nI2 =[I2] * 0,2
4 10-3 -x =[I2] * 0,2 soit x = 4 10-3 -[I2] * 0,2
| t(s) |
0 |
30 |
60 |
100 |
200 |
300 |
400 |
600 |
800 |
1000 |
1200 |
1400 |
| x mol |
0 |
0,8 10-3 |
1,3 10-3 |
1,6 10-3 |
2,2 10-3 |
2,5 10-3 |
2,8 10-3 |
3,2 10-3 |
3,4 10-3 |
3,56 10-3 |
3,64 10-3 |
3,72 10-3 |
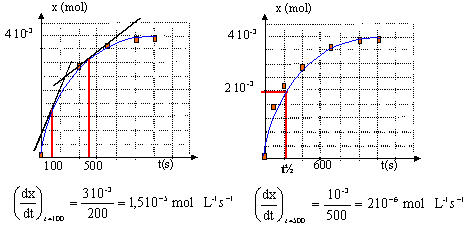
t½ voisin de 200 s, durée au bout de laquelle l'avancement est égal à la moitié de l'avancement final
la vitesse de la réaction ( coefficients directeurs des tangentes à la courbe) diminue au cours du temps car les concentrations des réactifs diminuent.
|
|
cinétique de la réaction des ion iodure avec l'eau oxygénée :
L'ion iodure est le réducteur du couple I2 (aq) / I- (aq). L'eau oxygénée, ou peroxyde d'hydrogène H2O2, est l'oxydant du couple H2O2 (aq) / H2O.
- Ecrire l'équation de la réaction d'oxydoréduction entre les ions iodure et l'eau oxygénée en milieu acide.
- Pour suivre la cinétique de la réaction, on commence par étonner le spectrophotomètre avec des solutions de diiode de concentration c connue. Les résultats sont regroupés ci-dessous.
| c mol/L |
1 10-4 |
2 10-4 |
4 10-4 |
6 10-4 |
8 10-4 |
10 10-4 |
| A |
0,188 |
0,378 |
0,749 |
1,128 |
1,501 |
1,878 |
- Tracer le représentation graphique A=f (c).
- Trouver son équation.
- La loi de Beer-Lambert est-elle vérifiée ?
- Pour étudier la réaction, on opère de la façon suivante.
- On prépare, dans un bécher, un volume v1 = 5,0 mL d'une solution S1 d'iodure de potassium de concentration c1=0,02 mol/L, auquel on ajoute 1 cristal de chlorure de fer (II). Les ions fer (II) permettent d'accélérer la réaction car les concentrations sont faibles. Ils n'intervient pas dans l'équation de la réaction.
- Dans un autre bécher, on place un volume v2=5,0 mL d'une solution S2 d'eau oxygénée acidifiée de concentration c2=2,0 x10-3 mol/L.
- A la date t=0, on mélange les contenus des 2 béchers et agite. Très rapidement, on place une partie du mélange dans une cuve que l'on introduit dans le spectrophotomètre. On relie le spectrophotomètre à un ordinateur et on obtient la courbe ci-dessous. 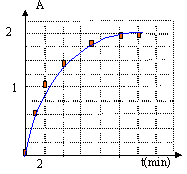
- Déduire de cette courbe, la représentation graphique [I2(aq)]=f(t) (on travaillera sur une dizaine de points).
- Quel est la réactif limitant ?
- Dresser le tableau d'évolution du système chimique.
- Dans la cuve du spectrophotomètre, la réaction avance de la même façon que dans le milieu réactionnel. Déterminer l'avancement x de la réaction en fonction de [I2 (aq)] et de V=v1+v2, volume total du mélange réactionnel. Calculer x pour les mêmes points que ceux utilisés dans la question 3.
- Tracer la représentation graphique x=f(t).
- Déterminer le temps de dem-réaction.
- Evaluer la vitesse de réaction aux dates t=2.0 minutes et t=6.0 minutes.
- Interpréter l'évolution de la vitesse.
corrigé
2I--->I2+2e- oxydation
H2O2 + 2H+ +2e---> 2H2O réduction
H2O2 + 2H+ +2I--->I2+2H2O
| c mol/L |
1 10-4 |
2 10-4 |
4 10-4 |
6 10-4 |
8 10-4 |
10 10-4 |
| A |
0,188 |
0,378 |
0,749 |
1,128 |
1,501 |
1,878 |
| A/c |
1880 |
1890 |
1872 |
1880 |
1876 |
1878 |
absorbance et concentration du diiode sont proportionnelles : la loi de Beer-Lambert est vérifiée.
A= 1880 c
à l'instant initial, les quantités de matière sont :
ion iodure : 0,02* 5 10-3 = 10-4 mol
eau oxygénée : 2 10-3 * 5 10-3 = 10-5 mol
|
|
H2O2 |
2I- |
I2 |
| initial |
10-5 mol |
10-4 mol |
0 |
| en cours |
10-5 -x |
10-4 - 2x |
x |
| fin |
10-5 -xmax=0 |
10-4 - 2xmax |
xmax=10-5 mol |
H2O2 est le réactif limitant.
à partir de la courbe A=f(t) on obtient [I2]=f(t) en divisant l'absorbance A par 1880.
[I2]= x / (v1+v2) = x / (5+5) 10-3 = 100 x d'où x = [I2]/100
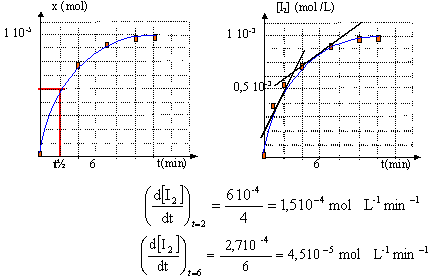
|
|
réduction du diiode
Le " lugol " est une solution antiseptique à base de diiode I2. Quand on plonge une lame de zinc dans cette solution, on peut observer, au bout d'un temps assez long, une décoloration et une attaque du zinc. L'équation de la réaction est : Zn (s) + I2 (aq) à Zn2+ (aq) + 2I- (aq)
Pour étudier cette réaction, on suit l'évolution de la quantité de matière de diiode présente en fonction du temps. Au bout de cette expérience, la température est de 20°C. La concentration initiale du diiode est c0=0,020 mol/L. On effectue 12 prélèvements de volume v0 = 20mL que l'on place dans 12 béchers. A la date t=0, on introduit, dans chaque bécher, deux morceaux de grenaille de zinc (le diiode est alors le réactif limitant). A chaque date indiquée dans le tableau ci-dessous, on place rapidement un des béchers dans la glace, puis on titre le diiode restant par une solution de thiosulfate de sodium de concentration c=0,020 mol/L.
L'équation de la réaction de titrage est : 2S2O32- (aq) + I2 (aq) --> S4O62-(aq)+ 2I- (aq).
Les résultats des titrages sont indiqués dans le tableau ci-dessous où véq représente le volume de sodium de thiosulfate de sodium versé à l'équivalence.
| t(s) |
30 |
60 |
100 |
200 |
300 |
400 |
600 |
800 |
1000 |
1200 |
1400 |
1600 |
| véq(mL) |
31,6 |
27,4 |
24,2 |
19 |
15,2 |
12,5 |
8,4 |
5,8 |
4,2 |
3,2 |
2,6 |
2,2 |
- Calculer la quantité de matière initiale de diiode notée n0.
- Exprimer nI2(aq), quantité de matière de diiode à la date t en fonction de c et de véq. Calculer nI2(aq), à chaque date. Regrouper les résultats sous forme d'un tableau.
- Dresser le tableau d'avancement de la réaction. En déduire une relation entre nI2(aq) restant à la date t, n0 et l'avancement x. Calculer x à chaque date. Regrouper les résultats sous forme d'un tableau.
- Tracer la représentation graphique x=f(t).
- Le diiode est le réactif limitant. Calculer l'avancement maximal, en déduire le temps de demi-réaction.
- On a placé les béchers dans la glace avant d'effectuer le titrage. Comment appelle-t-on cette opération ?
- Le thiosulfate de sodium est hydraté. Sa formule est Na2S2O3, 2H2O. Quelle masse de solide a-t-il fallu pour préparer 500 mL de solution de concentration 0,020 mol/L ?
-Faire le schéma annoté du montage qui sert au titrage.Comment détecter l'équivalence ?
corrigé
n0 =0,02 * 20 10-3 = 4 10-4 mol.
|
|
2S2O32- ajouté |
I2 |
S4O62- |
2I- |
| initial |
0 |
nI2 mol. |
0 |
0 |
| en cours |
c v = 0,02 v |
nI2 - 0,01 v |
0,01 v |
0,02 v |
| équivalence |
c véq = 0,02 véq |
nI2 - 0,01 véq=0 |
0,01 véq |
0,02 véq |
à la date t , nI2 = ½ cvéq = 0,01 véq
| t(s) |
30 |
60 |
100 |
200 |
300 |
400 |
600 |
800 |
1000 |
1200 |
1400 |
1600 |
| nI2 mmol |
0,316 |
0,274 |
0,242 |
0,19 |
0,152 |
0,125 |
0,084 |
0,058 |
0,042 |
0,032 |
0,026 |
0,022 |
Zn (s) + I2 (aq) à Zn2+ (aq) + 2I- (aq)
|
|
Zn (s) |
I2 |
| initial |
excès |
n0 |
| en cours |
|
n0 -x = nI2 |
| fin |
|
n0 -xmax=0 |
x = n0 - nI2 = 0,4 -nI2 mmol
| t(s) |
30 |
60 |
100 |
200 |
300 |
400 |
600 |
800 |
1000 |
1200 |
1400 |
1600 |
| x mmol |
0,084 |
0,126 |
0,16 |
0,21 |
0,25 |
0,28 |
0,32 |
0,34 |
0,36 |
0,37 |
0,375 |
0,38 |
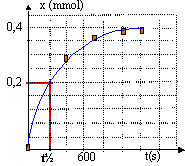
trempe ou blocage cinétique de la réaction
préparer 500 mL de chaque solution :
0,1 mol thiosulfate de sodium dans 0,5 L
masse molaire : 2*23+2*32+3*16+2*18 = 194g/ mol
donc peser : 194*0,01 = 1,94 g de solide puis dissoudre dans 0,5 L d'eau .
la burette contient la solution de thiosulfate de sodium de concentration connue.
le bécher contient la solution de diiode à doser + empois d'amidon ( en présence de diiode , l'empois d'amidon donne un couleur violette eintense)
agitateur magnétique.
|
|
L'ammoniac de format NH3 , est l'une des espèces chimiques les plus importantes industriellement. Il sert en effet à préparer des nettoyants ménagers, des engrais, des explosifs, des fibres textiles (par exemple, le nylon) …. Sa synthèse se fait en phase gazeuse à partir de diazote et de dihydrogène, à une température de 450 °C environ.
- Ecrire l'équation de la réaction.
- Pourquoi opère t on à une température élevée ?
- On peut étudier en laboratoire cette réaction en fermant un mélange de diazote et de dihydrogène dans un récipient muni d'un manomètre.Qu'est ce qu'un manomètre ? Comment évolue la pression du mélange au fur et à mesure que la réaction se produit, la température du réacteur restant constante ?
- Si l'on part d'un mélange de 25 moles de diazote et 75 moles de dihydrogène, quelle quantité de matière d'ammoniac peut on théoriquement obtenir ?
- Expérimentalement, on n'en obtient que 22 moles. Calculer le rendement de la réaction.
corrigé
3H2 + N2 = 2NH3.
la température est un facteur cinétique : la vitesse de la réaction augmente.
Le manomètre permet la mesure de la pression du mélange gazeux.
volume du réacteur et température constantes, comment évolue le nombre de moles ?
|
|
3H2 |
+ N2 |
= 2NH3 |
| initial |
75 |
25 |
0 |
| en cours |
75-3x |
25-x |
2x |
| final |
0 |
0 |
50 mol |
à la date t : 75-3x + 25-x+2x = 100-2x mol
or PV = nRT, si la quantité de matière en moles diminue alors la pression diminue.
rendement 22 / 50 = 44%.
|
|
On souhaite préparer une solution aqueuse d'hydroxyde de sodium, de concentration cb=0,10 mol/L, à partir d'une solution S1, de concentration c1 environ égale à 1,1 mol/L. On dilue S1, pour obtenir une solution S2 de volume V2=500 mL, dix fois moins concentrée que S1.
- Préciser le matériel nécessaire pour effectuer cette dilution dans les meilleures conditions de sécurité, en indiquant la suite logique des opérations à effectuer.
- Quelle est alors la concentration c2 de la solution S2 ?
- Pour vérifier la valeur de c2, on prélève un volume Vb=10,0 cm3 de la solution S2, que l'on titre par une solution aqueuse d'acide chlorhydrique, de concentration ca=0,100 mol/L, en présence de bleu de bromothymol. Le virage de l'indicateur coloré à lieu pour un volume équivalent Véquiv=12,5 cm3 de la solution d'acide versé.
- Faire un schéma du dispositif utilisé au cours du titrage, en nommant les instructions de verrerie.
- Ecrire l'équation chimique de la réaction du titrage.
- Déduire de la mesure de Véquiv la valeur de la concentration c2 de la solution S2.
- A partir de la solution S2, on prépare un volume V=250 cm3 de solution S d'hydroxyde de sodium, de concentration cb=0,10 mol/L, dans une fiole jaugée de contenance 250 mL. Quel volume v'b de S2 doit on utiliser ?
corrigé
facteur de dilution = 10 ; volume de la fiole jaugée = 500 mL, donc :
prélever 50 mL de la solution mère à l'aide d'une pipette de 50 mL + pipeteur
placer dans la fiole jaugée et compléter avec de l'eau distillée jusqu'au trait de jauge.
porter des lunettes de protection
c2 = 0,11 mol/L.
acide chlorhydrique de concentration connue dans la burette
10 mL solution S2 à doser dans le bécher ou dans un erlenmeyer + indicateur coloré
agitateur magnétique
H3O+ + HO- --> 2H2O
à l'équivalence du dosage d'un monoacide par une monobase : Ca Véqui = CbVb
soit Cb = 0,1*12,5 / 10 = 0,125 mol/L.
facteur de dilution = 0,125/0,1=1,25 ; volume de la fiole jaugée = 250 mL, donc :
prélever 250/1,25 = 200 mL de la solution S2 à l'aide d'une pipette ou d'une burette graduée
placer dans la fiole jaugée et compléter avec de l'eau distillée jusqu'au trait de jauge.
|
|
Le zinc réagit avec l'acide chlorhydrique : les produits de la réaction sont les ions Zn2+ et du dihydrogène.
- Ecrire l'équation chimique de la réaction.
- Quel couples oxydant / réducteur fait elle intervenir ?
- On plonge un petit morceau de zinc dans l'acide chlorhydrique et on étudie la cinétique de la réaction en mesurant, à l'aide d'une éprouvette graduée, le volume de dihydrogène produit au cours du temps, on obtient les résultats suivants :
| t (min) |
0 |
1 |
2 |
3 |
4 |
5 |
| V H2(mL) |
0 |
6,3 |
9,9 |
12 |
13,5 |
14,5 |
- Justifier que la technique de mesure utilisée est bien adaptée au suivi cinétique de la réaction.
- Tracer le graphe représentant la quantité de matière de dihydrogène formée en fonction du temps, sachant que le volume molaire dans les conditions de l'expérience est de 24 L/mol.
- Si on faisait la même expérience avec l'acide moins concentré, faudrait il plus ou moins de deux minutes pour recueillir 9,9 mL de dihydrogène ?
- Le volume de gaz produit au bout d'un temps très long sera-t-il le même pour les deux expériences.
- On utilise deux systèmes initiaux de compositions identiques, à la même température, avec dans un cas du zinc en poudre et dans l'autre cas du zinc en grenaille.
- On observe que le dégagement gazeux est plus important dans le système où le zinc est à l'état de poudre. Sachant que la réaction a lieu à la surface du métal, proposer une interprétation.
- Le volume gazeux obtenu à l'état final est il le même dans les deux cas ? Pourquoi ?
corrigé
couples redox Zn/Zn2+ et H+/H2.
Zn + 2H+-->Zn2+ +H2.
| t (min) |
0 |
1 |
2 |
3 |
4 |
5 |
| V H2(mL) |
0 |
6,3 |
9,9 |
12 |
13,5 |
14,5 |
| n H2(mmoL)= V/24 |
0 |
0,262 |
0,412 |
0,5 |
0,562 |
0,604 |
la réaction étant relativement lente il est possible de mesurer le volume du gaz sur une cuve à eau : H2 insoluble dans l'eau.
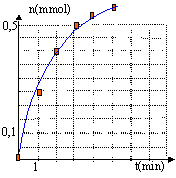
la concentration des réactifs est un facteur cinétique : la vitesse de la réaction augmente avec leur concentration.
si l'acide est moins concentré il faudra plus de deux minutes pour recueillir 9,9 mL de gaz.
Si le zinc est le réactif limitant, alors le volume de gaz obtenu sera le même
si l'acide moins concentré est le réactif limitant, le volume de gaz sera plus faible.
la réaction chimique se fait à la surface du métal : plus celle-ci est grande ( solide en poudre) , plus la vitesse de la réaction est importante. L'état final sera plus rapidement atteint.
Par contre l'état final sera identique, si les quantités initiales de réactifs sont les mêmes.
|
|
On étudie la transformation lente de réduction des ions peroxodisulfate S2O82- (aq) par les ions iodure I- (aq). Ces deux réactifs appartiennent aux couples oxydant / réducteur S2O82- (aq) / SO42- (aq) et I2(aq)/ I-(aq)
- Ecrire l'équation chimique de la réaction.
- On mélange 10 mL d'une solution aqueuse de peroxodisulfate de sodium [S2O82- ] = 1,0 10-2 mol/L et 10 mL d'une solution aqueuse d'iodure de calcium, on concentration molaire en ions iodure [ I-] = 0,01 mol/L. Effectuer un bilan de matière à l'état final.
- On renouvelle l'expérience avec 10 mL d'une solution aqueuse dont la soluté est du peroxodisulfate de sodium, Na2S2O8 (s) de concentration massique cm=2,38g/L, et 10 mL d'une solution aqueuse dont le soluté est de l'iodure de calcium, Cal2 (s), de concentration massique c'm = 2,94 g/L. La température du système est la même que précédemment.
- Effectuer un bilan de matière à l'état final.
- Pour quelle valeur de l'avancement ce système se trouve t il dans le même état que l'état final du système précédemment étudié ?
- Lequel des deux systèmes atteint cet état le plus rapidement ?
- Sachant que le diiode est une espèce colorée en solution aqueuse, proposer une méthode de suivi temporel de la transformation.
Masses molaires atomiques M(Na)=23g/mol M(S)=32,1 g/mol M(O)=16g/mol M(Ca)=40 ,1 g/mol M(I)=126,9 g/mol
corrigé
S2O82- + 2I--->2SO42- + I2
|
|
S2O82- |
+ 2I- |
2SO42- |
I2 |
| initial |
10-4 mol |
10-4 mol |
0 |
0 |
| en cours |
10-4 -x |
10-4 -2x |
2x |
x |
| fin |
5 10-5 mol |
0 |
10-4 mol |
5 10-5 mol |
dans le cas des solides : concentration massique (g/L) / masse molaire (g/mol) * volume (L)= Qté de matière (mol)
Ca I2(s) --> Ca2+ + 2I-.
donc nI- = 2 *2,94/294*0,01 =
|
|
S2O82- |
+ 2I- |
2SO42- |
I2 |
| initial |
10-4 mol |
2 10-4 mol |
0 |
0 |
| en cours |
10-4 -x |
2 10-4 -2x |
2x |
x |
| fin |
0 |
0 |
2 10-4 mol |
10-4 mol |
ce second système atteint l'état final du premier système ( exception faite de l'ion iodure)
lorsque l'avancement vaut x= 5 10-5 mol.
la vitesse de la réaction est plus grande si la concentration des réactifs est plus importante: le second système atteint cet état le plus rapidement.
le suivi de l'évolution de la réaction peut être effectué par spectrophotométrie : suivi de l'évolution de la couleur brune du diiode.
|
- On dispose d'une solution d'acide chlorhydrique de pH=2,9 obtenue en dissolvant un volume gazeux V de chlorure d'hydrogène par litre de solution.
- Ecrire l'équation de la réaction de dissolution du chlorure d'hydrogène dans l'eau.
- Déterminer la quantité nH+, dion oxonium présent dans 1 L de solution.
- Calculer le volume V de gaz dissout. (volume molaire : Vm=23,8 L/mol)
- On considère d'autre part 1 L de solution d'acide éthanoïque dont le pH vaut 2,9, obtenue en dissolvant 0,1 mol d'acide éthanoïque par litre de solution. On notera C1 la concentration de cette solution.
- Déterminer la quantité n1, dion oxonium présent dans 1 L de solution.
- Quel est le taux d'avancement final ?
- Ecrire l'équation qui traduit la réaction de l'acide éthanoïque avec l'eau.
- On dilue la solution d'acide éthanoïque de concentration C1 pour obtenir 100 mL d'une solution de concentration molaire C2 = 0,01 mol/L.
- Indiquer les opérations à réaliser pour cette dilution.
- Le pH de la solution diluée est 3,4. Quel est le taux d'avancement final ?
- Déterminer la quantité n2 d'ion oxonium présents dans cette solution diluée. Comparer n1 et n2 et conclure quant à l'effet d'une dilution.
- Si on effectuait la même dilution sur la solution d'acide chlorhydrique de pH=2,9, quel serait le pH de la solution diluée ?
corrigé
HCl(g) + H2O --> H3O+ + Cl-.
pH= - log [H3O+] ou bien [H3O+] = 10-pH = 10-2,9 = 1,26 10-3 mol/L.
Quantité de matiére de chlorure d'hydrogéne dissout : 1,26 10-3 mol
volume de gaz (L) = Qté de matière (mol) fois volume molaire (L/mol) = 1,26 10-3 *23,8 = 0,03L.
nH+ = 1,26 10-3 mol/Lsoit environ100 fois plus petit que la concentration C1.
|
|
CH3COOH |
+H2O |
= CH3COO- |
+ H3O+ |
| initial |
0,1 |
solvant |
0 |
0 |
| en cours |
0,1-x |
|
x |
x |
| final |
0,1-xmax =0 |
|
xmax =0,1 mol |
xmax =0,1 mol |
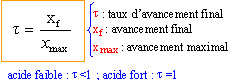
t = 1,26 10-3 / 0,1 = 1,26 10-2 (1,26%)
facteur de dilution = C1 / C2 = 10
volume fiole jaugée / volume pipette = 10
prélever 10 mL de la solution mère de concentration C1 à la pipette graduée + pipeteur
placer dans une fiole jaugée de 100 mL et compléter avec de l'eau distillée jusqu'au trait de jauge.
pH= 3,4 donc n2 = xf = 10-3,4 = 4 10-4 mol/L
xmax= 0,01 mol/L
t = 4 10-4 / 0,01 = 4 10-2 (4%)
règle de Le Chatelier ou règle de modération:
en ajoutant de l'eau (un réactif) on déplace l'équilibre dans le sens "comsommation de l'eau", c'est à dire dissociation de l'acide faible en ion oxonium et éthanoate.
par dilution, un acide faible se rapproche du comportement d'un acide fort.
en diluant 10 fois la solution initiale d'acide chlorhydrique (acide fort), la concentration en ion oxonium est divisée par dix et le pH augmente d'une unité pH ( soit 2,9+1=3,9)
| |
| 1
résistance de l'air
trajectoire
énergie
|
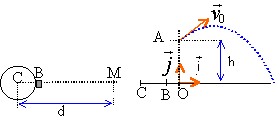
En 1990 ,'américain Randy Barnes établit le record du mondede lancer du poids : la distance atteinte est d= 23,12 m. Le poids est constitué par une sphère homogène métallique lisse de masse m= 7,26 kg. L'aire de lancement est constituée d'un cercle métallique de diamètre D= 2,14 m et par un butoir B. La portée du jet est mesurée à partir du centre C du cercle.
A l'issue de la phase d'élan le pois est abandonné en A, à la hauteur h= 2m au dessus du sol horizontal, à la distance BO= 0,35 m en avant du butoir B. Le bras qui lance fait alors un angle de 45° avec l'horizontale. Cet angle est celui de la direction du vecteur vitesse initiale v0 avec l'horizontale.
Choix d'un modèle :
La résultante des forces de frottements dues à l'air est donnée par : R= ½ r Cx S V² où r est la masse volumique de l'air 1,9 10-3 kg /m3, S l'aire de la section équatoriale de la sphère 1,13 10-2 m², Cx un coefficient caractéristique de la forme de l'objet Cx = 0,5 S.I et V la valeur de la vitesse.
- Montrer que la grandeur Cx est sans dimension.
- Montrer que l'on peut négliger la résistance de l'air vis à vis de la pesanteur agissant sur le "poids" sachant qu'au cours du mouvement la vitesse est de l'ordre de 10 m/s.
Etude du mouvement :
- Les frottements sont négligeables. Etablir les équations horaires du mouvement du poids dès l'instant où celui ci est abandonné en A. Donner l'équation de la trajectoire dans le repère donné (expressions littérale et numérique) en fonction de v0.Quel est la nature du mouvement projeté sur chaque axe.
- Vérifier que la vitesse initiale est voisine de 14 m /s.
- Déterminer la durée du trajet du poids entre a et M. En déduire la vitesse au moment du contact avec le sol.
aspect énergétique:
- Déterminer l'énergie cinétique fournie au poids par l'athlète au moment du lancer.
- L'origine des énergies potentielles étant fixée au niveau du sol horizontal, déterminer l'expression de l'énergie mécanique du poids au moment du lancer. En déduire l'expression de la valeur de la vitesse au point de chute. Le résultat est-il en accord avec le résultat précédent.
corrigé
|
|
|
R force en newton ou masse fois accélération R : [kg] [m] [s]-2.
masse volumique r :[kg] [m]-3.
surface S : [m]²
vitesse au carré : V² en [m]² [s]-2.
soit rSV² en [kg] [m][s]-2.
donc Cx sans dimension.
R= 0,5 *1,29 * 0,5 *1,13 10-2 *100 = 0,364 N
poids : mg = 7,26*9,1 = 71,2N très supérieur (200 fois) à R.
vitesse initiale : [V0 cos 45 ; V0 sin 45 ]
accélération de la pesanteur : [ 0, -g]
position initiale [0 ; 2 ]
vitesse à une date t : [V0 cos 45 ; -gt +V0 sin 45]
position à une date t : x = V0 cos 45 t ; y = -½ gt² +V0 sin 45t + h
trajectoire : y = - ½ gx² / (V0 cos 45)² + x tan 45 + h
y = -9,8 x² / V0² + x + 2
le mouvement est rectiligne uniforme sur l'axe des abscisses.
le mouvement est uniformèment accéléré sur l'axe des ordonnées.
au point d'impact sur le sol : x = 23,12 - 1,07 - 0,35 = 21,7 m
0 = -9,81 *21,7² / V0² +21,7 +2 d'où V0 = 13,95 m/s.
durée du déplacement AM :
xM= 21,7 m soit 21,7 = 14 * cos 45 t d'où t = 2,19 s.
vitesse au point d'impact :
Vx = 14*cos45 = 9,9 ; Vy = -9,8*2,19 + 14*sin 45 = -11,58
V² = 9,9 ² + (-11,58)² = 232,19 d'où VM = 15,23 m/s.
énergie cinétique initiale : ½mV0² = 0,5*7,26 *14² = 711,4 J
énergie potentielle initiale : mgh = 7,26*9,8*2 = 142,4 J
énergie mécanique initiale : ½ mV0² + mgh
énergie mécanique finale (point d'impact) :½ mVM²
conservation de l'énergie mécanique :
½ mV0² + mgh = ½ mVM²
VM² = V0² + 2gh = 14² +2*9,8*2 = 235,2 d'où VM= 15,33 m/s.
résultat cohérent avec celui trouvé ci dessus.
|
|
Cet exercice étudie un modèle très simplifié du mouvement du centre d'inertie G d'un skieur dans différentes phases de son parcours. Masse du skieur m= 80 kg.
Montée et plat:
L'ensemble des forces de frottement est assimilé à une force unique, de sens opposé au vecteur vitesse, de norme constante F=50N. Le skieur reste constamment en contact avec le sol.
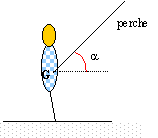
- Afin de monter au sommet de la piste, le skieur se présente sur l'aire de départ horizontale. Initialement immobile, il s'accroche àune perche faisant un angle a=45°, constant avec l'horizontale. La perche exerce une force de traction dirigée suivant sa propre direction. Après un parcours de longueur 8m, la vitesse se stabilise à la valeur v0= 2 m/s.
- Faire l'inventaire de toutes les forces s'exerçant sur le skieur pendant la phase de démarrage. Les représenter sur un schéma.
- Calculer l'accélération du skieur durant la phase de démarrage.
- Déterminer l'expression littérale puis numériquement de la force constante T exercée par la perche sur le skieur.
- Le skieur toujours tiré par la perche, monte à vitesse constante (2m/s) une pente rectiligne inclinée de b=40° par rapport à l'horizontale. La perche forme un angle d=30° avec le sol. Après avoir schématisé le skieur, déterminer littérallement puis numériquement l'intensité de la force T exercée par la perche sur le skieur.
- Le skieur arrive au sommet avec la vitesse précédente, sur une plate forme horizontale où il lâche la perche. Combien de temps mettra-t-il pour s'arrèter? Quelle distance aura t-il parcouru sur la plate forme ?
descente:
- Le skieur participant à un concours de vitesse, s'élance, à partir du repos sur une piste rectiligne inclinée de b'= 28° par rapport à l'horizontale. En admettant l'existence de force de frottement de même valeur qu'à la montée, quelle vitesse atteindrait-il après 300 m de parcours ?
- La vitesse mesurée n'est en fait que de 107 km/h. En déduire l'intensité moyenne de la force de frottement supposée constante qui s'exerce sur le skieur au cours de la descente.
- La valeur de la force de frottement varie en fait avec la vitesse suivant la loi F=kv². On prendra k= 0,33 N s² m-2. Le coefficient k dépend en particulier de l'aérodynamisme du skieur. Quelle est la limite de la vitesse maximale que le skieur pourrait atteindre sur une piste suffisamment longue.
Peut-il ainsi espérer battre le reccord du monde de vitesse ? (248 , 1 km/h)
corrigé
|
| démarrage :
système : lskieur et équipement; référentiel terrestre galiléen.
Ecrire la seconde loi de Newton, le skieur étant soumis à son poids, à l'action de la perche, à l'action du sol .
projeter cette relation vectorielle sur un axe horizontal à droite.
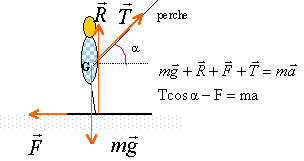
T= (ma +F)/ cosa.
calcul de l'accélération : v0² -v² init = 2a d avec v init = 0
a = v0² / (2d) = 2² / (2*8)= 0,25 m/s².
T= (80*0,25+50) / cos45 = 99N.
montée à vitesse constante :
D'après le principe d'inertie la somme des forces est nulle.
projection suivant un axe parallèle au plan vers le haut
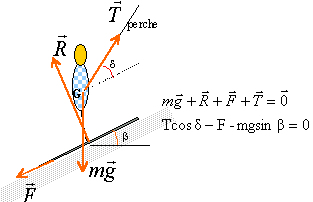
T = (F+mgsinb) / cosd.
T=(50+80*9,8*sin40) / cos30 = 639 N.
plate forme horizontale :
théorème de l'énergie cinétique( seul fes frottements travaillent)
½ mv²fin- ½ mv²0 = -fd
fd=½ mv²0 d'où d = 0,5*80 * 2² / 50 = 3,2 m.
mouvement rectiligne uniformément freiné.
v²fin- v²0 ==0- v²0 2ad d'où a = - v²0 / (2d) = -4 / 6,4 = -0,625 m/s².
d = -½ at² + v0t ou mieux v = at + v0.
t =(v-v0) / a = (0-2) / (-0,625) =3,2 s.
plate forme horizontale :
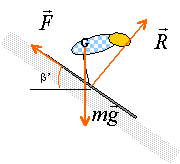
projection de la somme des forces sur un axe parallèle au plan dirigé vers le bas :
mgsinb'-f = ma
a = gsinb'-f /m = 9,8 * sin28 -50/80 = 4,6 - 0,625 = 3,975 m/s².
v² -0 = 2ad
v² =2*3,975 *300 = 2385 et v = 48,8 m/s =175,8 km/h.
le poids et les forces de frottement travaillent
(mgsinb' -f) AB
variation d'énergie cinétique : ½mv² avec v = 107 /3,6 = 29,72 m/s
théorème de l'énergie cinétique : ½mv² = (mgsinb' -f) AB
mv² / (2AB) = mgsinb' -f
f = mgsinb' -mv² / (2AB)
f= 80[9,8*sin28 -29,72² / 600] = 250N.
lorsque la vitesse limite est atteinte la somme des forces appliquées au skieur est nulle.
Projection de cette somme sur un axe parallèle au plan dirigé vers le bas :
mgsinb'-f = 0 avec f = kv²
v² = mgsinb' / k = 80*9,8 sin28 / 0,33 = 1115
vitesse limite = 33,4 m/s = 33,4*3,6 = 120,28 km/h.
|
|
aspect historique
|
On appelle pendule simple un système constitué d'un objet dense, de masse m, suspendu à un fil inextensible, de longueur l et de masse négligeable devant m, accroché à une extrémité fixe ; la taille de l'objet est négligeable devant l. On se propose dans cet exercice d’étudier différents aspects de ce modèle physique.
Aperçu historique: Extrait de « Discours et démonstrations » de Galilée (1564-1642).
Il s’agit d’une discussion entre Salviati (Galilée ) et Sagrédo (l'un de ses élèves). Salviati : Pour obtenir un premier pendule dont la durée d'oscillation soit le double de celui d'un second pendule, il convient de donner au premier une longueur quadruple de celle du second. Sagrédo: Si j'ai bien compris, je pourrais donc aisément connaître la longueur d'une corde, quand bien même son point de suspension serait invisible et que l'on apercevrait seulement son extrémité inférieure. Si en effet j'attache en cette partie de la corde, une « masse » fort lourde, à laquelle je communique un mouvement de va et vient, et si un ami compte le nombre de ses oscillations pendant que moi-même je compte les oscillations effectuées par un autre pendule suspendu à un fil mesurant exactement une coudée, alors grâce au nombre des oscillations de ces deux pendules pendant une même durée, je trouverai la longueur de la corde ; supposons par exemple que mon ami ait compté vingt oscillations de la grande corde, dans la même durée où j'en comptais deux cent quarante pour mon fil long d'une coudée ..
- L’affirmation de Salviati.On considère qu’une oscillation correspond à un mouvement d’aller et de retour - menu du pendule. Quelle grandeur physique est désignée par l’expression « la durée d’une oscillation » ? Montrer qu’une seule des propositions suivantes satisfait à l’affirmation de Salviati : "La durée d’oscillation est proportionnelle"
* à l'inverse de 1a longueur .
* au carré dela longueur.
* à la racine carrée de la longueur.
- La réponse de Sagrédo : on note respectivement l1 et T1 la longueur et la durée d'une oscillation du pendule de Sagrédo, l2 et T2 la longueur et la durée d'une oscillation du pendule de l'ami de Sagrédo. On admet qu'une coudée équivaut à 50 cm : l1 = 50 cm.. En utilisant la réponse de Sagrédo, déterminer la valeur numérique du rapport T2 /T1. Calculer la longueur l2 .
corrigé
|
|
|
La durée d'une oscillation est la période .
Celle ci est proportionnelle à la racine carrée de la longueur.
Le rapport des 2 périodes est égal au rapport des racines carrée des 2 longueurs.
Le rapport des périodes vaut 12.
Le rapport des longueurs vaut racine carrée de 12 soit 3,46.
puis 3,46 *0,5 =1,73 m, longueur du pendule le plus long
|
| 2
influence de la masse et de la longueur
|
Étude expérimentale.
- On se propose maintenant d’étudier expérimentalement l’influence de différents paramètres sur la durée d’une oscillation d’un pendule simple. Pour cela, on utilise un fil inextensible de longueur l et de masse considérée comme nulle. Les objets denses de masse m, suspendus au fil, sont suffisamment petits pour que leur taille soit négligeable devant l. Le pendule ainsi constitué est écarté de sa position d’équilibre d’un angle q 0 petit (inférieur à 10°) puis lâché sans vitesse initiale. On obtient alors des oscillations libres amorties dont la durée d'une oscillation ou pseudo-période est notée T. On mesure à l’aide d’un chronomètre la durée t nécessaire au pendule pour réaliser 20 oscillations.
Influence de la masse.
On réalise une série de mesures de .t avec un fil de longueur l = 24,4 cm et différents objets de
masse m. On obtient les mesures suivantes :
| masse (g) |
60 |
125 |
160 |
200 |
| temps(s) |
19,9 |
19,8 |
19,9 |
19,9 |
Que peut-on en déduire quant à l’influence de la masse sur la pseudo-période du pendule ?
Influence de la longueur.
On suspend maintenant un objet de masse m = 125 g et on fait varier la longueur du fil. On obtient
les mesures suivantes :
| longueur (cm) |
12,3 |
24,4 |
28,6 |
32,4 |
38,5 |
| temps(s) |
14,1 |
19,8 |
21,4 |
22,8 |
24,9 |
Quel est le graphique le plus simple à exploiter ?
La relation littérale entre T et l peut alors s’écrire T = k la. Donner les valeurs de a et k.
corrigé
|
|
|
La période est indépendante de la masse fixée au fil..
Un graphique simple à exploiter est une droite. Les grandeurs physiques sont proportionnelles et le coefficient directeur de la droite donne le coefficient de proportionnalité.
prendre la racine carrée de la longueur.
| racine carrée de la longueur exprimée en mètre |
0,351 |
0,501 |
0,535 |
0,57 |
0,62 |
| temps(s) |
14,1 |
19,8 |
21,4 |
22,8 |
24,9 |
| temps / rac carée (L) |
40,1 |
39,5 |
39,4 |
40 |
40,1 |
temps = 40 * longueur 0,5.
temps =20 périodes
période = 2 * longueur 0,5.
|
| 3
influence de la valeur du champ de pesanteur
|
On ne peut pas modifier la valeur g du champ de pesanteur. Toutefois, grâce à un pendule oscillant sans frottement sur un plan incliné d'un angle a sur l'horizontale tout se passe comme si le pendule était vertical et placé dans un champ de pesanteur de valeur g’ tel que :
g’ = g . sin a avec g = 9,8 m . s -2 .
Description du dispositif : sur une table inclinée d'un angle a par rapport à l'horizontale, un petit mobile autoporteur de masse m = 125 g est suspendu à un point fixe, par un fil de longueur l = 24,4 cm.
Pour différentes valeurs de a (on modifie alors la valeur de g’), on mesure la durée t de oscillations de faible amplitude. On obtient les mesures suivantes :
| a en degré |
90 |
70 |
50 |
30 |
20 |
10 |
| t en seconde |
19,9 |
20,6 |
22,6 |
28,2 |
33,9 |
46,5 |
| g' -0,5 |
0,32 |
0,33 |
0,36 |
0,45 |
0,55 |
0,77 |
- Tracer, sur papier millimétré, la courbe représentative des variations de T en fonction de g' -0,5
- Donner, sous forme littérale, l'équation de cette courbe. Conclusion.
- La pseudo-période peut se mettre sous la forme : T =C racine carrée de (L/g) où C est une constante. Montrer que C est une grandeur sans dimension. Déterminer la valeur de C à partir de la valeur de k obtenue ci dessus.
corrigé
|
|
|
Le
|
- La force de gravitation s'exerçant entre la terre et le soleil vaut F=3,5 1022 N. Connaissant la constante de gravitation G=6,67 10-11 SI, la masse de la terre Mt =6 1024 kg et la distance terre soleil d=1,5 108 km, exprimer en fonction des données la masse Ms du soleil puis calculer sa valeur numérique.
- Un satellite assimilé à un point matériel de masse m décrit d'un mouvement uniforme dans le champ de gravitation de la terre une orbite circulaire à l'altitude h= 400 km. L 'orbite est située dans le plan équatorial de la terre et le rayon terestre a pour valeur R=6400 km.
- Déterminer dans le repère géocentrique la vitesse V du satellite en fonction de G, Mt et r ( r étant le rayon de la trajectoire). Calculer la valeur numérique de V.
-Déterminer dans le même repère, les expressions littérales et les valeurs numériques de la période T et de la vitesse angulaire w du satellite.
- Le mouvement de ce satellite obéit à la troisième loi de Képler qui a pour expression ( choisir l'expression correcte)
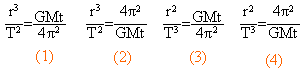
- Déterminer en fonction de Mt, G, R et T=86400s (période de révolution de la terre sur son axe), l'altitude h0 à laquelle un satellite en orbite circulaire équatoriale autour de la terre doit évoluer pour qu'il soit géostationnaire.Calculer la valeur numérique de h0.
corrigé
|
| force de gravitation proportionnelle aux masses et inversement proportionnelle au carré de la distance
F = G Mt Ms / d² masse en kg et distance en m.
d = 1,5 1011 m
Ms = F d² / ( G Mt) = 3,5 1022 * 10,5² 1022 / (6,67 10-11*6 1024) = 1,96 1030 kg.
Le satellite est soumis uniquement à la force de gravitation centripète F=G Mt m / r²
le mouvement est circulaire uniforme.
l'accélération normale est égale à : aN= V² / r
la relation fondamentale de la dynamique ( 2ème loi de Newton) projetée sur l'axe n de la base de frenet donne :
V² / r = G Mt / r²
d'où V² = G Mt / r avec r = (6400+400) 103 = 6,8 106 mètres
V² = 6,67 10-11 * 6 1024 / 6,8 106 = 5,88 107.
V=7668 m/s.
la période est la durée nécessaire pour parcourir une circonférence à la vitesse V
2pr = V T
4p²r² = V² T²
remplacer V² par l'expression ci dessus.
4p²r² =G Mt T² / r
soit T² = 4 p² r3 / (G Mt) ( 3ème loi de Kepler)
l'expression (1) est correcte.
T² = 4*3,14² * (6,8 106)3 / (6,67 10-11*6 1024) d'où T= 5558 s.
la vitesse angulaire est égale à : w = 2p / T = 6,28 / 5558 = 1,13 10-3 rad/s.
r3 = T² G Mt / (4 p²) d'après la 3ème loi de Képler.
avec r = R +h0.
r3 = (8,64 104 )² *6,67 10-11*61024 /( 4*3,14²) = 75,75 1021 m3.
r = 4,237 107 m = 42370 km
h0= 42300-6400= 35970 km.
|
|
Le Grand Accélérateur National d'Ions Lourds GANIL permet d'accélérer des ions lourds fortement chargés. Le GANIL comporte : un cyclotron injecteur (C0) relié à une source d'ions ; deux cyclotrons identiques (CSS1) et (CSS2) qui accélèrent les ions fournis par le cyclotron injecteur (C0) ; un "éplucheur" d'ions situé entre les cyclotrons (CSS1) et (CSS2), dont le rôle sera étudié dans la partie 2 de cet exercice. On considère qu'il ne modifie pas l'énergie cinétique des ions le traversant.
.
Dans cette partie, on considère un ion de charge q positive et de masse m arrivant dans le cyclotron(C0) au point A, centre du dispositif, avec une vitesse considérée comme nulle. Le poids de l'ion est négligeable devant les autres forces. Le cyclotron (C0) est constitué de deux demi-cylindres D1 et D2 en forme de "D" séparés par un espace étroit. À l'intérieur de chaque "D" règne un champ magnétique B , uniforme et constant, perpendiculaire au plan de la figure. Dans l'intervalle situé entre les deux "D" règne un champ électrique E associé à la tension u. Sous l'action de ces deux champs, le mouvement de l'ion dans le cyclotron a une trajectoire dont une partie (de A à A6 ) a été représentée.
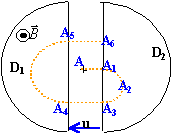
Action du champ magnétique:
- Représenter, en justifiant, au point A2 de la trajectoire de l'ion dans le cyclotron, le vecteur vitesse v2 de l'ion et la force magnétique Fm qui s'exerce sur l'ion. En déduire le sens du champ magnétique B , le représenter.
- Montrer que l'action du champ B ne permet pas d'accroître l'énergie cinétique de l'ion de vecteur vitesse v . On précise que dans un "D", le mouvement de l'ion est circulaire uniforme et on rappelle que dans un "D" le rayon de la trajectoire est R = mv /q.B .
- Montrer que la durée de passage, notée tP , dans un demi-cylindre ne dépend pas de la valeur v de la vitesse de l'ion.
Etude de la tension u :
Pour accroître l'énergie cinétique de l'ion, on utilise l'action du champ électrique E résultant de la tension u appliquée entre les deux "D". On considère que pendant la durée très courte de passage de l'ion d'un "D" à l'autre, la tension u reste constante.
- Déterminer, en fonction de q et u les expressions des variations de l'énergie cinétique de l'ion respectivement entre A3 et A4 puis entre A5 et A6. En déduire si la tension u doit être alternative ou continue. Justifier la réponse.
- On peut négliger la durée de passage de l'ion dans l'intervalle entre les deux "D" devant la durée tP de passage de l'ion dans un demi-cylindre. Parmi les tensions représentées indiquer, en justifiant votre réponse, la ou les tensions permettant d'obtenir une accélération de l'ion à chaque passage dans l'intervalle entre les deux "D" (à t0 = 0, l'ion passe au point A1).
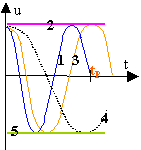
corrigé
|
|
|
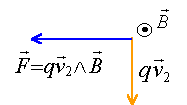
La force magnétique perpendiculaire à la vitesse ne travaille pas et en conséquence ne modifie pas la norme de la vitesse de l'ion.
mouvement uniforme dans un "D" alors la demi circonférence parcourue est proportionnelle à la durée du parcours .
p R= v tP d'où tP= p R / v = p m /(qB) indépendant de la vitesse.
entre A3 et A4 : travail de la force électrique q (V3-V4). =q(-u)
ce travail doit être positif pour qu'il y ait augmentation de la vitesse
DEc=qu
entre A5 et A6 : travail de la force électrique q (V5-V6). = q(u)
cette expression est l'opposée de la valeur précédente
ce travail doit être positif pour qu'il y ait augmentation de la vitesse, donc la tension doit changer de signe (tension alternative).
L'accélération sera efficace si la durée de passge entre les "D" correspond à une demi période de la tension alternative.
les courbes 2 et 5 correspondant à des tensions continues sont à éliminer.
les demi périodes des courbes 1 et 3 ne correspondent pas à tP, donc courbes à éliminer.
la demi période de la courbe 4 est égale à tP : bonne courbe.
|
| 2
éjection
|
- Après chaque passage dans l'intervalle entre les deux "D", le rayon R de la trajectoire de l'ion dans un "D" augmente. On considèrera que lorsque ce rayon finit par atteindre le rayon R0 d'un "D" du cyclotron (C0), l'ion est alors éjecté du cyclotron (C0).
- Exprimer en fonction de m, q, B et R0 l'énergie cinétique EC(0) de l'ion lors de son éjection du cyclotron (C0).
- Calculer, en MeV, l'énergie cinétique EC(0) d'un ion zinc Zn 11+ (onze plus) sachant que : B = 1,67 T ; m = 1,06 × 10 -25 kg ; R0 = 0,465 m ; e = 1,60 × 10 -19 C ; 1 eV = 1,60 × 10 -19 J.
corrigé
|
|
|
énergie cinétique de l'ion éjecté : 0,5 mv² avec mv/(qB)=R0.
Ec = (qBR0)²/ (2m)
q=11*1,6 10-19 C
Ec = (11*1,6 10-19 *1,37*0,465)²/2,12 10-25=59,3 10-13 J
puis diviser par 1,6 10-19 : 37,06 106 eV
puis diviser par 106 :37,06 MeV
|
| 3
rôle de l'éplucheur d'ions
|
Dans la suite, on admet que le principe de fonctionnement des cyclotrons CSS1 et CSS2 est identique à celui du cyclotron (C0). Par conséquent, la relation établie pour l'énergie cinétique de l'ion en fonction de q, m, B et R (rayon de la trajectoire circulaire de l'ion dans un "D") reste valable pour le mouvement de l'ion dans les cyclotrons CSS1 et CSS2. Pour que le cyclotron CSS2, identique au cyclotron CSS1, joue son rôle d'accélérateur des ions zinc, il faut modifier une caractéristique de l'ion zinc. Un moyen économiquement rentable consiste à modifier la charge de l'ion zinc : c'est le rôle de l'éplucheur.
- Indiquer, en justifiant la réponse, si la charge de l'ion zinc doit diminuer ou augmenter lors de son passage dans l'éplucheur situé entre les cyclotrons CSS1 et CSS2.
- A la sortie du cyclotron CSS1, l'ion Zn 11+ , d'énergie cinétique EC(1) = 310 MeV, traverse l'éplucheur d'ions dans lequel sa charge est modifiée. Puis il pénètre avec l'énergie cinétique EC(1) dans le cyclotron CSS2 identique à CSS1 (même valeur du champ magnétique et même rayon des "D"). Dans CSS2 l'ion zinc, de masse m = 1,06 × 10 -25 kg, est accéléré et sort du cyclotron CSS2 avec une énergie cinétique EC(2) = 1,60 × 10 3 MeV. Déterminer la formule de l'ion zinc qui pénètre dans le cyclotron CSS2 après passage par l'éplucheur d'ions.
corrigé
|
|
|
La vitesse de l'ion est proportionnelle à la charge de l'ion. v=R q B /m
Augmenter la vitesse c'est augmenter la charge de l'ion. C'est à dire enlever des électron.
La masse de l'électron étant très inférieure à celle des nucléons, la masse de l'ion varie très peu.
Ec(1) =(q1BR)² /(2m) =310 MeV
Ec(2) =(q2BR)² /(2m) =1600 MeV
diviser Ec(2) par Ec(1) puis prendre la racine carrée
1600 / 310 = (q2 / q1 )²
q2 / q1 =2,27 avec q1 =11
q2 = 25 charges
|
|
Une chambre d'ionisation produit des ions 20Ne+ et 22Ne+ de masses respectives m1et m2. Le poids est négligeable devant les forces électromagnétiques et leur mouvement a lieu dans le vide.
Les ions pénetrent avec une vitesse initiale négligeable dans un accélérateur où ils sont soumis à un champ électrique uniforme crée par une tension U0=VM-VN établie entre 2 plaques conductrices M et N . On désigne par v1 et v2 les vitesses des ions 20Ne+ et 22Ne+ lors du passage en O1. charge élémentaire e=1,6 10-19 C.
- Représenter sur un schéma le vecteur champ électrique et donner le signe de U0. Justifier.
- Exprimer la vitesse de l'ion 20Ne+ à la sortie de l'accélérateur en fonction de sa masse et de U0.
- Calculer cette vitesse si la valeur absolue de la tension vaut 2 104 V; masse atomique molaire de l'ion 20Ne+ =0,02 kg mol-1; nombre d'Avogadro = 6,02 1023 mol-1.
- Montrer qu'en O1 : m1v1² =m2 v2² ; en déduire la valeur de v2.masse atomique molaire de l'ion 22Ne+ =0,022 kg mol-1.
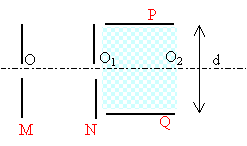
- Au delà de O1 les ions entrent dans un sélecteur de vitesse limité par les plaques P et Q. Dans cette région ils sont soumis simultanémentà un champ électrique uniforme crée par une tension positive U=VQ-VP et à un champ magnétique perpendiculaire aux vecteurs vitesses et au champ électrique. Représenter les champs sur un schéma afin que les forces électriques et magnétiques soient opposées.
- On règle la tension U de telle façon que le mouvement des ions 20Ne+ soit rectiligne et uniforme de trajectoire O1O2. Représenter les forces qui agissent sur l'autre ion 22Ne+ ainsi que le vecteur vitesse v1.
- Exprimer U en fonction de v1, d (distance des plaques P et Q) et du champ magnétique. Calculer U si B=0,1 T et d=5 cm.
- Dans quelle direction seront déviés les ions 22Ne+ . Justifier le nom "filtre de vitesse" donné à la région limitée par P et Q.
corrigé
|
|
|
Entre O et O1 les ions sont accélérés : seule la force électrique travaille, donc son travail est moteur :
q UMN >0
La charge q est positive donc UMN >0 soit VM >VN.
Le champ électrique pointe vers le plus petit potentiel donc vers N.
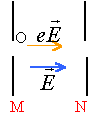
le théorème de l'énergie cinétique s'écrit entre M et N:
0,5 m1v1² =eU0.
v1² =2eU0 / m1.
caluler la masse en kg : 0,02/ 6,02 1023 = 3,322 10-26 kg
v1² = 2*1,6 10-19 *2 104 / 3,322 10-26 = 1,928 1011
v1 = 4,39 105 m s-1.
même travail pour l'autre ion :0,5 m2v2² =eU0.
m1v1² = m2v2² =2eU0
v2² =m1/m2 v1² d'où v2 = 4,186 105 m s-1.
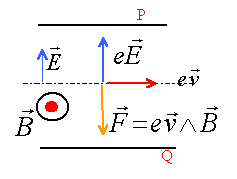
La tension UQP est positive : le champ électrique pointe vers le plus petit potentiel soit vers P
la charge q est positive, alors la force électrique a le sens du champ électrique.
la force magnétique opposée (mouvement uniforme) à la force électrique pointe vers Q.
le vecteur charge fois vitesse pointe vers la droite.
La règle de la main droite donne le sens du champ magnétique.
Le mouvement de l'ion 20Ne+ étant rectiligne uniforme, la somme des forces est nulle.
la norme des forces est égale
eE=ev1B ou E=U / d = v 1B soit U= d v 1B
distance en mètre d=0,05 m
U=0,05*4,39 105 *0,1 = 2195 V.
mouvement de l'ion 22Ne+ :
la force électrique ne dépend que de la charge et de la tension U, elle n'est pas modifiée
la force magnétique est proportionnelle à la vitesse de l'ion : or cet ion plus massif a une vitesse plus faible que v1. La force magnétique sera plus petite que la force électrique .
La somme des forces n'est pas nulle, elle est égale à une force verticale dirigée vers P, de norme constante.
Le mouvement de cet ion 22Ne+ sera uniformément accéléré : la trajectoire sera un arc de parabole.
cet ion ne pourra pas sortir par le trou O2, ( tant qu'on ne modifie pas la tension U) il va heurter la paroi du sélecteur de vitesse.
Seuls les ions O1 sortiront par le trou O2.
|
|
étude graphique
énergie
frottements
|
Dans un plan horizontal, on considère un système oscillant formé d'un mobile autoporteur lié à deux points fixes par l'intermédiaire de deux ressorts élastiques identiques, de masses négligeables, et de même axe. Le système, initialement au repos, est écarté de sa position d'équilibre en déplaçant le centre d'inertie G du mobile le long de l'axe des deux ressorts. L'ensemble des deux ressorts est équivalent à un ressort de constante de raideur k = 15,4 N.m-1.
rappel : l'élongation y d'un oscillateur linéaire sans amortissement satisfait à l'équation différentielle y"+w²y =0, dont les solutions y(t) sont sinusoïdales, de pulsation w.
Une table à numériser permet la détermination des positions successives y de G dans un repère lié à la table ; la trajectoire de G est portée par l'axe y' y . Un logiciel de traitement de données permet d'afficher les points correspondant aux couples (t,y), (t,), ou toute autre fonction souhaitée, et d'en représenter les courbes.
1. Dans toute cette partie, le mobile a pour masse m = 220 g et le système considéré est non amorti.
- . La figure ci dessous représente l'ensemble des points d'enregistrement (t,y). Ces points se situent sur une courbe d'allure sinusoïdale. Déterminer graphiquement la valeur de la période T et de l 'élongation maximale Ym de y. A partir de la valeur de T, calculer la pulsation de de cet oscillateur.
- La courbe ci dessous, représente les couples (y,y" ). Montrer que ce graphique est en accord avec l'équation différentielle proposée. Que représente le coefficient directeur de la droite support de cet ensemble de points ? Déterminer graphiquement sa valeur et en déduire l'ordre de grandeur de la pulsation de l'oscillateur .
- Les valeurs expérimentales de la pulsation déterminées ci dessus sont-elles compatibles avec la valeur théorique de la pulsation propre w0 de cet oscillateur ?
- . Ecrire la relation de conservation de l'énergie E pour un oscillateur se déplaçant en translation, sans frottement. Montrer qu'elle peut s'écrire y'² / w0 ² +y² =C, où C est une constante qui s'exprime en, fonction de E et de k. Exprimer C en fonction de Ym et calculer sa valeur.
- Pour traduire la conservation de l'énergie de l'oscillateur sur un graphe, on peut utiliser les représentations des couples
 t,E) ou (y², y'² / w0 ²). Reporter sur votre feuille les deux représentations choisies parmi les trois proposées, en précisant les grandeurs portées sur les axes. t,E) ou (y², y'² / w0 ²). Reporter sur votre feuille les deux représentations choisies parmi les trois proposées, en précisant les grandeurs portées sur les axes.
2. Les ressorts étant inchangés, un dispositif d'amortissement est désormais fixé sur le mobile. On réalise un nouvel enregistrement, représenté ci dessous.
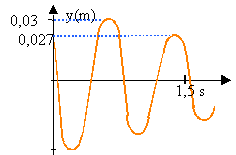
En utilisant deux valeurs consécutives de la valeur maximale de y, donner un ordre de grandeur du pourcentage de l'énergie perdue par l'oscillateur au cours d'une période. Quelles sont les causes physiques de la dissipation ?
corrigé
|
|
|
deux périodes sont égales à 1,5 s (lecture graphe)
T=0,75 s.
la pulsation w est égale à 2p / T=6,28 /0,75 = 8,37 rad s-1.
l'amplitude Ym est égale à 0,04 m.
l'équation différentielle peut s'écrire : y" = -w²y
fonction linéaire décroissante de coefficient directeur -w².
déterminer ce coefficient à partir du graphique : -4 /0,06 = -66,66
d'où w = 8,16 rad s-1.
valeur théorique wo²= k/m =15,4 /0,22 =70 soit wo =8,36 rad s-1
en accord avec les valeurs précédentes
l'énergie mécanique est la somme de l'énergie potentielle élastique et de l'énergie cinétique
E = 0,5 ky² + 0,5 my'²
E = 0,5 k ( y² + m/k y'²) avec wo²= k/m
2E / k = C = (y² +y'² / w0 ²)
Lorsque y =Ym alors toute l'énergie est sous forme potentielle élastique.
E = 0,5 kY²m
l'énergie mécanique se conserve .
E = 0,5 kY²m = 0,5k (y² +y'² / w0 ²)
C = Y²m = 0,04² = 0,0016 m²
E en fonction du temps, fonction constante : graphe (2) avec E en ordonnée
C = (y² +y'² / w0 ²) s'écrit : y² = C- y'² / w0 ².
fonction affine décroissante donc graphe (1) avec y² en ordonnée
du fait des frottements mécaniques, l'oscillateur s'amorti; l'énergie mécanique diminue au cours du temps. Lorsque y =Ym, toute l'énergie est sous forme potentielle élastique, proportionnelle à Y²m.
à la date t : E1= 0,5 k 0,03² = 0,5*15,4*0,03²= 6,93 mJ
à la date t+T, E2 =0,5 k 0,027² =0,5*15,4*0,0027²= 5,61 mJ
diminution d'énergie : 1,32 mJ soit environ 19%
alors que l'amplitude ne diminuait que de 10%.
|
|
oscillations libres
|
La suspension d'un véhicule permet d’atténuer les vibrations verticales qui nuisent au confort et à la sécurité des passagers, par exemple lors du passage du véhicule dans un trou sur une route. Elle est constituée au niveau de chaque roue d’un ressort et d’un amortisseur (voir figure 1). On note G le centre d’inertie du véhicule. Lorsqu’on écarte le véhicule de sa position d’équilibre Go et qu’on le lâche, il oscille autour de cette position. L’amplitude des oscillations décroît suivant le degré d’amortissement de la suspension. L’ensemble du véhicule est équivalent à un oscillateur mécanique unique vertical amorti de masse m, de raideur k.
On étudie le mouvement du centre d'inertie G seulement suivant la verticale. On repère son ordonnée y sur un axe Oy orienté vers le haut. La position du centre d'inertie du système à l’équilibre Go ( ressorts comprimés) est prise pour origine O de l'axe.
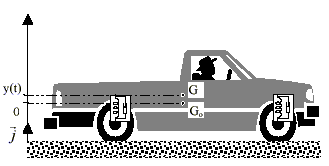
Données :
•Masse : m = 1,5 × 10 3 kg.
•Constante de raideur du ressort équivalent k = 6,0 × 10 5 N.m -1 .
•La force de frottement qui s’exerce sur la masse m est opposée à la vitesse du point G suivant la verticale, on peut l'écrire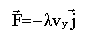
vy est la composante verticale de la vitesse du point G par rapport à l’axe de la roue.
l est une constante positive appelée coefficient d'amortissement ou de frottement.
On s'intéresse par la suite à l'influence de ce coefficient d'amortissement sur la qualité de la suspension.
I. Oscillations libres de la suspension
Le document ci dessous donne trois courbes représentant y = g(t) pour trois véhicules dont seules les valeurs du coefficient d’amortissement sont différentes :
| Courbe n°1 |
Courbe n°2 |
Courbe n°3 |
| l1= 1,5 × 10 4 kg.s -1 |
l2= 5 × 10 4 kg.s -1 |
l3= 1,5 × 10 5 kg.s -1 |
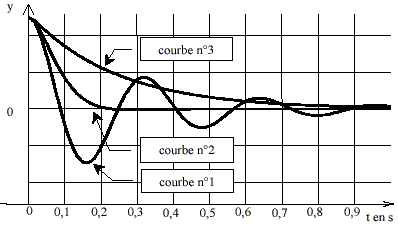
- Expliquer pourquoi les courbes n°1 et n°3 correspondent respectivement aux coefficients d’amortissement l1 et l 3 .
- L’une des courbes du document 1 est une sinusoïde amortie dont on définit la pseudo-période comme étant la durée entre deux maxima consécutifs. Déterminer graphiquement la valeur de cette pseudo-période T.
- Le régime critique est le meilleur pour le confort et la sécurité des passagers. Quelle valeur du coefficient d'amortissement convient le mieux parmi les trois valeurs proposées ?
corrigé
|
|
|
La courbe 1, la moins amortie (pseudopériodique) correspond au cefficient d'amortissement le plus faible l1.
La courbe 3, la plus amortie (régime apériodique) correspond au cefficient d'amortissement le plus grand l3.
pseudopériode lue sur le graphe (courbe 1) = 0,32 s.
Le régime critique corespond à la courbe 2 avec l2= 5 × 10 4 kg.s -1
|
| 2
oscillations forcées
|
2. Test des amortisseurs, oscillations forcées
Pour tester chacun des amortisseurs, on soumet les roues à une même excitation sinusoïdale produite par un support placé sous chaque roue .
L’amplitude Ym des oscillations du centre d'inertie G du véhicule dépend alors de deux facteurs : l’amplitude YE et la fréquence fE de l’excitation sinusoïdale. La résolution des questions suivantes ne demande aucune mise en équation. On admettra que le comportement qualitatif du système s’apparente à celui d’un oscillateur amorti soumis à une force excitatrice sinusoïdale.
L’amplitude YE de l’excitation sinusoïdale est maintenue constante.
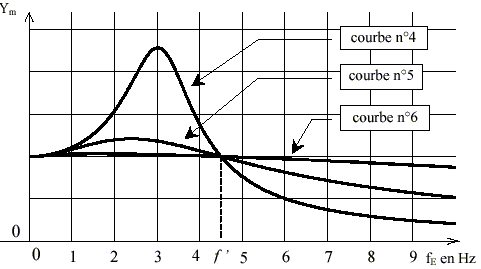
Le document ci dessus donne les courbes représentant Ym=g(fE) pour les trois valeurs du coefficient d’amortissement du paragraphe 1.
- Pourquoi est-il important de préciser que l’amplitude YE de l’excitation est maintenue constante ?
- Que peut-on dire de l’amplitude Ym à la résonance ?
- Pour le véhicule équipé de l'amortisseur de coefficient le plus faible, déterminer graphiquement la fréquence de résonance fr . Comparer sa valeur à la fréquence propre de l’oscillateur mécanique {masse, ressort}. On prend 1 / p =0,3.
- Préciser à l’aide des courbes ci dessus si la fréquence de résonance est fonction du coefficient d'amortissement.
- À la fréquence excitatrice f ’ = 4,5 Hz, l’amplitude des oscillations Ym est la même pour les trois oscillateurs. Quel amortisseur faut-il choisir pour équiper le véhicule sachant que plus l’amplitude des oscillations est faible, meilleure est la qualité des amortisseurs :
•pour les fréquences excitatrices fE telles que fE < f ’ ?
•pour des fréquences excitatrices fE > f ’ ?
Quel amortisseur donne le meilleur compromis quelle que soit la fréquence excitatrice ?
(Justifier chaque réponse)
corrigé
|
|
|
l'amplitude Ym passe par un maximum à la résonance.
courbe 4 : la fréquence à la résonance est égale à 3 Hz
période propre de l'oscillateur = 2p racine carré (m/k)
T= 2p rac carée(1500/6 105)=2p rac carrée (2,5 10-3)=0,314 s
fréquence propre : 1/0,314 =3,18 Hz
en accord avec la valeur trouvée sur le graphe.
courbe 5 : la fréquence de résonance est proche de 2,5 Hz, donc la fréquence de résonance dépend du coefficient d'amortissement.
pour les fréquences excitatrices fE telles que fE < f ’ , pour l'amortisseur correspondant à la courbe 6 (amortissement le plus grand soit l3) l'amplitude des oscillations est la plus faible.
pour des fréquences excitatrices fE > f ’ , l'amortisseur correspondant à l1 (amortissement le plus faible) donne des oscillations de faibles amplitudes.
l'amortisseur correspondant à l2 (amortissement moyen) donne un phénomène de résonance de faible amplitude et au delà de fE, les amplitudes des oscillations sont moins importantes qu'avec un oscillateur très amorti. Cet amortisseur donne le meilleur compromis.
|
|
A l'occasion des Jeux Olympiques de l'été 1996, une revue scientifique faisait état des dernières méthodes de dépistage du dopage. On y décrivait une nouvelle méthode en voie d'homologation, mettant en jeu la spectrométrie de masse, dont le principe est donné ci-après.
Le dopage par les stéroïdes anabolisants administrés aux sportifs pour que leurs muscles se développent serait assez facile à dépister. Pourtant des stéroïdes anabolisants, notamment la testostérone, l'hormone mâle, sont naturellement présents dans l'organisme : comment faire la différence entre l'hormone naturelle et l'anabolisant interdit ?
On propose une méthode fondée sur la spectrométrie de masse isotopique, où l'on détermine le rapport des concentrations en carbone 13 (13C) et en un de ses isotopes le carbone 12 (12C). En effet, les rapports qui caractérisent les matières premières utilisées pour la préparation de la testostérone de synthèse et les molécules biosynthétisées par l'homme à partir de son alimentation, sont différents.
On propose dans cette méthode de mesurer le rapport des concentrations en carbone 13C et en carbone 12C du dioxyde de carbone provenant de la combustion de l'hormone extraite d'un prélèvement d'urine de l'athlète contrôlé, par la technique de la spectrométrie de masse. Le déplacement des particules dans les chambres d'accélération et de déviation s'effectue dans le vide
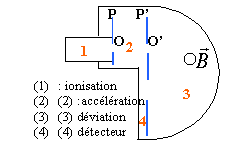
1. Accélération.
- La chambre d'ionisation (1) produit des ions 12CO2+ de masse m1 et des ions 13CO2+ de masse m2. On néglige les forces de pesanteur dans la suite du problème ; le mouvement des ions est rapporté au référentiel du laboratoire considéré galiléen. Les ions 12CO2+ et 13CO2+ pénètrent dans le chambre d'accélération en O avec une vitesse initiale considérée comme nulle ; ils sont soumis à un champ électrique, supposé uniforme, de vecteur entre les plaques P et P' et sortent de la chambre en O' avec respectivement des vitesses de valeurs v1 et v2 . Représenter sur un schéma le vecteur champ électrique et justifier la réponse.
- En appliquant le théorème de l'énergie cinétique à l'ion 12CO2+, exprimer v1 en fonction de sa masse m1, de la charge élémentaire e et de la tension U0 = Vp - Vp'.
- En O', quelle relation vérifient v1 et v2
- Calculer les valeurs numériques de v1 et v2 .
Données : |Uo|=4000V; m1=7,31 10-26 kg; m2 = 7,47 10-26 kg ; e=1,6 10-19 C
2. Déviation.
es ions 12CO2+ et 13CO2+ pénètrent en O' dans une zone où règne un champ magnétique uniforme, de vecteur perpendiculaire au plan de la figure, permettant d'atteindre la plaque détectrice (4).
- Représenter surun schéma le vecteur champ magnétique permettant le mouvement circulaire uniforme des ions dans la direction attendue. Justifier la réponse.
- Montrer que pour la particule chargée de masse m, animée de la vitesse v1 de charge électrique e dans le champ magnétique uniforme de valeur B défini précédemment, le rapport donnant le rayon r de la trajectoire est homogène à une longueur. On admettra : [tesla] = [kg][s] -1 [C] -1.
- Exprimer le rayon r en fonction de m, e, Uo et B.
- En déduire le rapport des rayons des trajectoires des ions 12CO2+ et 13CO2+ en fonction de leurs masses m1 et m2 et les positions I1 et I2 des points d'impact des ions de masse m1 et m2. Les placer sur un schéma.
- Exprimer la distance I1I2 en fonction de m1, m2, e, U0 et B.
- Calculer la distance sachant que B = 0,25 T.
3. Résultat d'un contrôle.
L'analyse des impacts a permis de dénombrer les atomes 12C et 13C contenus dans les ions arrivés sur le détecteur pendant une certaine durée.
Les résultats des comptages effectuées à partir des échantillons d'urine de deux athlètes A et B sont rassemblés dans le tableau suivant et à compléter.
|
|
N1(12C) |
N2(13C) |
R=N2 / N1 |
d |
dopage |
| athlète A |
2231 |
24 |
|
|
oui |
non |
| athlète B |
2575 |
27 |
|
|
oui |
non |
| étalon standart |
2307 |
25 |
|
|
|
|
On y fait figurer également les comptages réalisés à partir d'un étalon standard international.
Les résultats des équipes de recherche sur cette méthode font référence à un coefficient défini par la relation : d=1000(R-Rstandart) / Rstandart avec R=N2 / N1.
Les nombres d'atomes de carbone 12 et 13, respectivement N1 et N2, donnés dans le tableau, tiennent compte de corrections dues, en particulier, à la présence d'isotopes de l'oxygène. On considère que l'athlète s'est dopé si la valeur du coefficient d est notablement inférieure à -27.
A partir des données du tableau, déterminer s'il y a eu dopage pour les athlètes A et B.
corrigé
|
|
|
le travail de la force électrique doit être positif, car la particule chargée doit être accélérée entre O et O'.
travail de cette force = eUOO'
la charge étant positive, le potentiel de O' doit être plus petit que celui de O. (UOO' positive)
Le champ électrique est dirigé vers les plus petits potentiels.
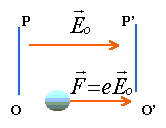
La variation d'énergie cinétique entre O et O' est égale au travail de la force électrique.
L'énergie cinétique initiale est voisine de zéro.
0,5m1v1² = eUOO'= eU0.
de même pour l'ion de masse m2 : 0,5m2v2² = eUOO'= eU0.
0,5m1v1² = 0,5m2v2² = eU0.
v1² =2eU0/m1 = 2*1,6 10-19 *4 103 / 7,31 10-26 =1,75 1010
v1 =1,32 105 m s-1. v2 =1,309 105 m s-1.
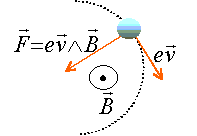
rayon = mv /(eB)
masse : kg ; vitesse : m s-1; e en coulomb ; B en tesla.
rayon =[kg] [m ][s]-1[C]-1[T]-1.
avec [T]-1= [kg]-1[s][C]
d'où rayon = [m ] homogène à une longueur.
r² = m²v² /(e²B²) avec mv²=2eU0.
r² = 2 m/e U0 / B²
r1 /r2 = racine carée (m1 / m2).
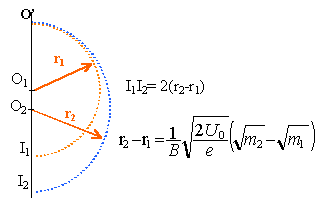
I1I2= 2/0,25 rac carrée(8000/1,6 10-19)( rac carrée(7,47 10-26)-rac carrée(7,31 10-26)
I1I2=8*2,23 1011*(2,733-2,703)10-13
I1I2= 5,2 mm.
|
|
N1(12C) |
N2(13C) |
R=N2 / N1 |
d |
dopage |
| athlète A |
2231 |
24 |
1,0757 10-2
|
-7,3 |
|
non |
| athlète B |
2575 |
27 |
1,0485 10-2
|
-32,4 |
oui |
|
| étalon standart |
2307 |
25 |
1,0836 10-2
|
|
|
|
|
|
Le montage représenté ci-dessous permet l’étude de l’établissement du courant dans un circuit comportant une bobine d’inductance L et de résistance r et une résistance R.
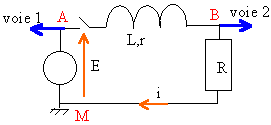
Données :U=E= 3,8 V ; R=50 ohms.
Un ordinateur muni d’une carte d’acquisition permet d’enregistrer l’évolution des tensions U aux bornes du générateur et uR aux bornes de la résistance R. À t=0 l’interrupteur est fermé et l’acquisition commence. Le document (A) ci-après représente le graphe de ces tensions en fonction du temps.
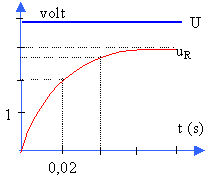
- Donner l’expression de la tension visualisée sur la voie 2 en fonction de l’intensité.
- Donner la valeur numérique de I , intensité dans le circuit en régime permanent.
- Établir la relation notée (1) entre E, L, r , R, i et di/dt. En déduire une expression littérale de I.
- Calculer la résistance r de la bobine.
- On modélise l’intensité du courant circulant dans le circuit au cours de son établissement sous la forme i= i (1-exp(-kt)) . Les paramètres de modélisation donnés par l’ordinateur sont
I=59,114 10-3 et k= 59,585. (le nombre de chiffres donnés est celui de l’ordinateur ; les unités sont celles du système international ; la précision des mesures ne correspond pas à celle de l’affichage). La constante de temps du circuit est : t = L / (R+r).
* Quelle est la dimension de k ? Justifier.
*En utilisant la relation kt =1, calculer la valeur numérique de L.
- Avec le montage utilisé précédemment, on réalise quatre expériences ; la valeur de U reste la même et on fait varier les valeurs de R et L ; les valeurs qui sont données à R permettent maintenant de négliger r .
On rappelle que l’intensité atteint 63 % de sa valeur maximale au bout d’une durée égale à t . Les courbes donnant l’évolution de l’intensité du courant au cours du temps pour ces expériences sont simulées à l’ordinateur et sont représentées sur le document ci-après : 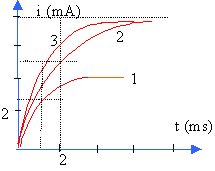
- Sachant que la courbe 1 correspond à R=1000W, déterminer la valeur de l’intensité en régime permanent, la constante de temps du circuit et l’inductance de la bobine.
- Recopier le tableau, remplir l’ensemble des cases vides et préciser le numéro de la courbe qui doit figurer sur la première ligne.
| n° de la courbe |
... |
1 |
... |
| I (mA) |
... |
... |
7,6 |
| R ohms |
500 |
1000 |
... |
| t (ms) |
... |
... |
... |
| L (H) |
... |
.... |
1 |
corrigé
|
|
|
Sur la voie 2 on visualise la tension aux bornes d'une résistance. La tension et l'intensité sont proportionnelles : uR = Ri = 50 i.
En régime permanent, la bobine alimentée par un générateur de tension constante se comporte comme une résistance de valeur r et uR= 3 V d'où I=3 /50 = 0,06 A.
Aux bornes de dipoles en série les tensions s'ajoutent et leur somme est égale à E
E = Ri + ri +L di/dt (1).
Lorsque le régime permanent est établi , di / dt =0 et E=(R+r) I
R+ r = 3,8 /0,06 = 63,3 W soit r = 13,3 W.
Le produit kt est sans dimensions ; k s'exprime en s-1 , inverse d'un temps.
t = 1 / 59,585 = 0,0168 s
t = L / (R+r ) d'où L= 0,0168*63,3 = 1,06 H
étude de la courbe 1
I voisin 4 mA;
à t = t , l'intensité est égale à : 4*0,63 = 2,5 mA
lecture graphique t voisin de 1 ms = 10-3 s.
L = Rt =1000 *0,001 =1 H
étude de la courbe 2
I voisin 8 mA (même valeur pour la courbe 3) donc R = 3,8 / 0,008 voisin 475 W.
à t = t , l'intensité est égale à : 8*0,63 = 5 mA
lecture graphique t voisin de 2 ms = 2 10-3 s.
L = Rt =500 *0,002 =1 H
étude de la courbe 3
I voisin 8 mA donc R = 3,8 / 0,008 voisin 475 W.
à t = t , l'intensité est égale à : 8*0,63 = 5 mA
lecture graphique t voisin de 1 ms = 10-3 s.
L = Rt ; 1 = 500 *0,001 soit L= 0,5 H.
| n° de la courbe |
3 |
1 |
2 |
| I (mA) |
7,6 |
4 |
7,6 |
| R ohms |
500 |
1000 |
500 |
| t (ms) |
1 |
1 |
2 |
| L (H) |
0,5 |
1 |
1 |
|
|
Chers élèves voici le site dont tout un chacun recherchait !
Vous l'avait beaucoups recherché?
Alors des élèves du pays l'ont realisé pour vous !
vous pouvez aussi proposer des exercices
en ajoutant des commentaires
salut et bonne visite |
 |
Vous pouvez donner votre opinion sur des exercices
enfin d'y apporter des solutions. |
 |
Vous pouvez aussi proposer des exercices
pour l'enrechissement du site et pour nous permettre
de bien satisfaire les demandes et besoins des élèves. |
 |
Ce site est le premier site d'exercices totalement gratuit au senegal . |
 |
Il a été créé en 2008 par des élèves en classe de 1ère au lycée des parcelles assainies(LPA). |

|


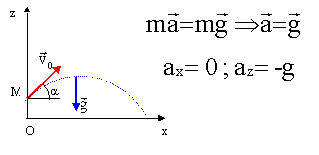




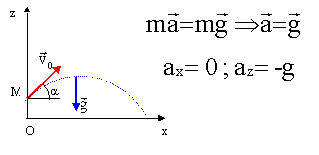
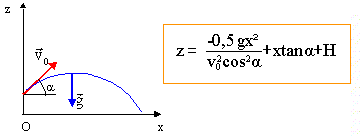
 3
3
 4
4